永田先生の『多変量解析法入門』の最後の内容になりました。最後の内容は多段抽出法でデータマイニングの一種とも考えられる分析法です。
多段分析法ではモデルを設定しないので、さほど複雑な内容ではありません。1つずつみていきましょう。
多段層別分析で用いるサンプル
まずは多段層別分析で用いるデータについて解説します。
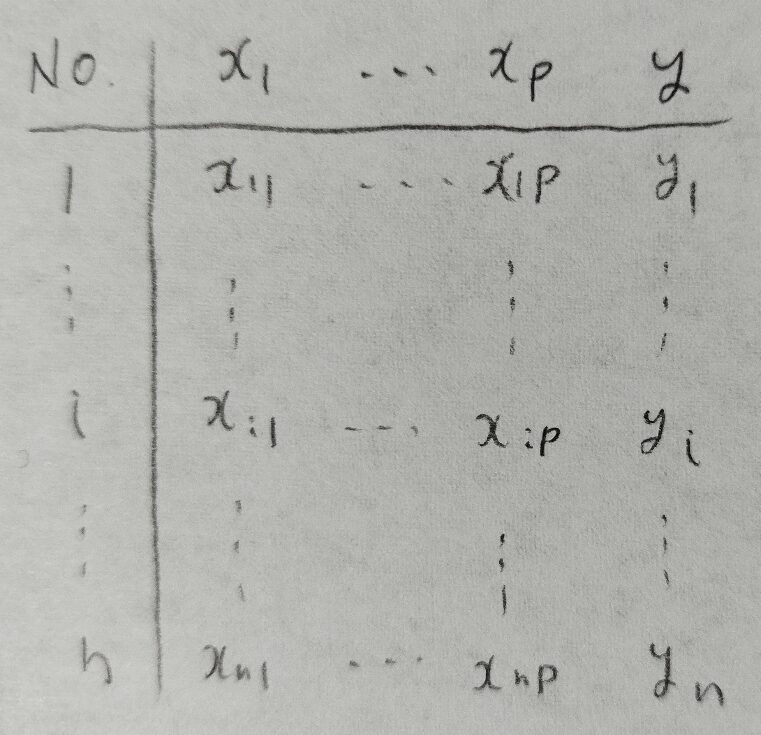
なんだか重回帰分析などに似ていますね。
そうですね!ただし多段層別分析の目的は重回帰分析とは異なります。
多段層別分析ではモデルを想定せずに考えます。サンプルサイズが大きいときに、サンプルの分類を目的として、目的変数yの違いをできるだけ際立たせる説明変数を用いてサンプルを2分割していきます。
2進木解析法の考え方
サンプルを2分割していく方法について解説します。これは2進木解析法の考えに基づきます。

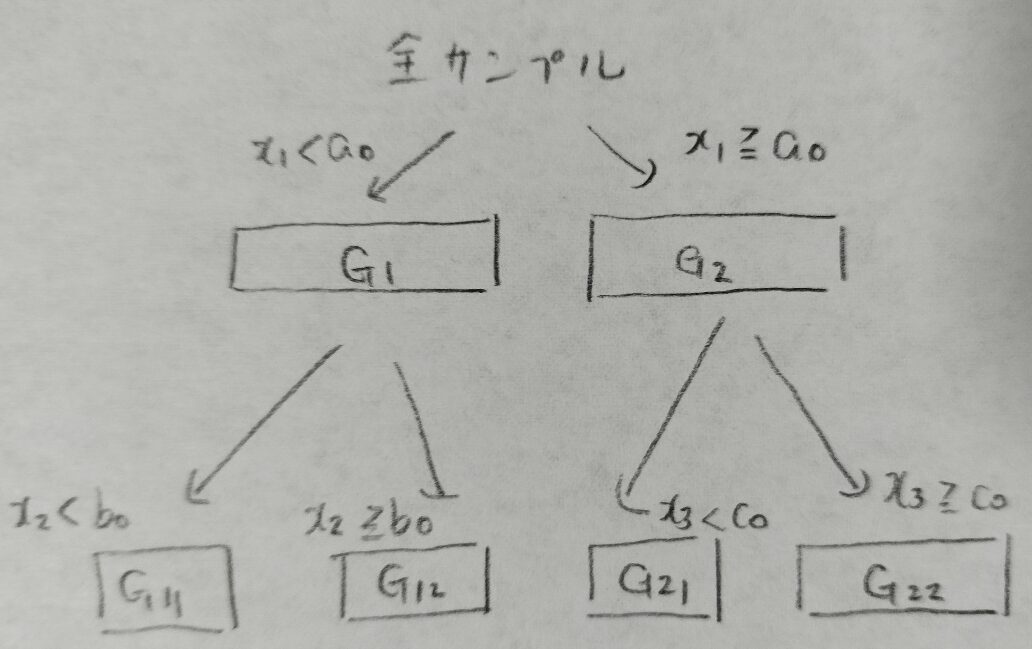
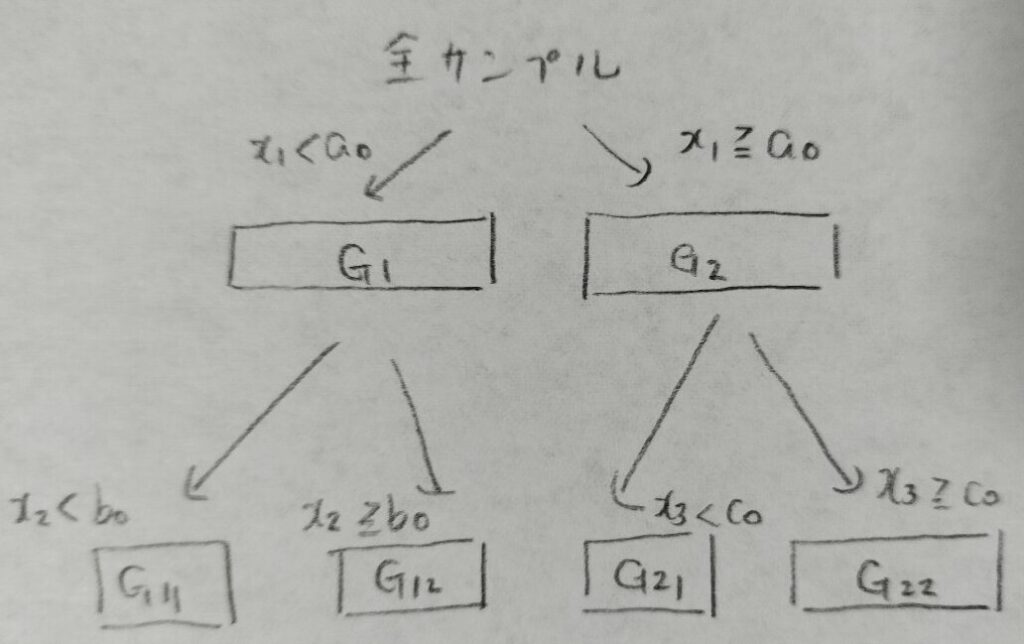
図03はyの違いという観点から最もよく分割できる説明変数をグループごとに選定して、グループごとに分割点を定めていく2進木解析法の1例の図です。
決定木の問題は統計検定1級に過去に出題されていますね!
2進木解析法での説明変数と分割点の判定法
多段層別分析でyの違いを際立たせるということなので「違い」という観点からF値を考えれば良さそうですね。
その通りです。図04のF値は2つの母平均の差の検定で用いる検定統計量の2乗です。このF値をすべての説明変数とそれぞれの説明変数の分割方法に関して計算し、F値が最も大きくなる説明変数とその分割点を用いて全サンプルを2グループに分けます。

ただし、この分析法を続けると果てなくグループが分かれていってしまうので分割の停止条件が必要になります。
①最終グループの個数の最大値を決めておきます。
②各最終グループに含まれるサンプルサイズの最小値を決めておきます。
③分割を行わないF値の下限を定めておきます。
目的変数が2個データの場合の分析法
たとえば目的変数yが1と2のみを取る場合を考えます。この時は2つの母不良率の差の検定で用いる検定統計量の2乗を考えればOKです。
要するに「違い」を考えたければF値を考えればOKということですね!
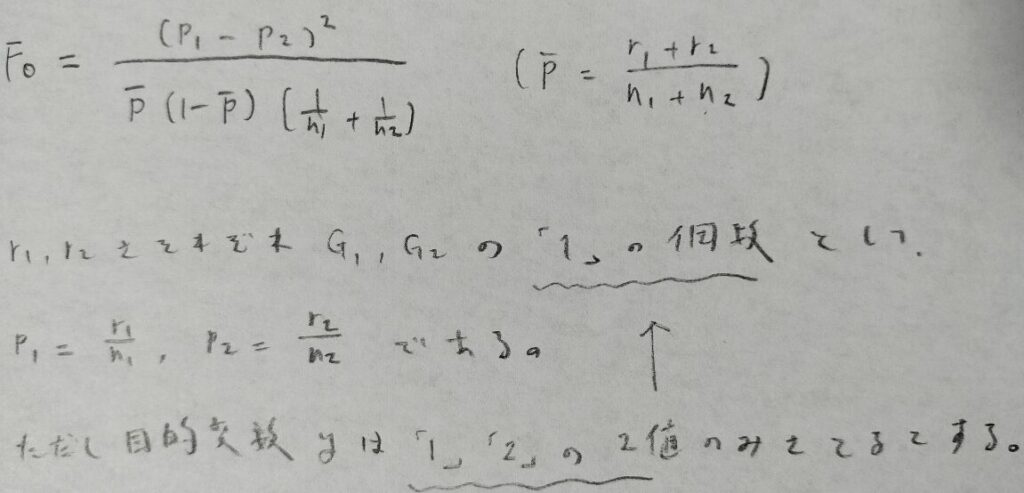
解析の考え方は、先ほどのF値とは異なる値となる点を除いて、まったく同様となります。
これで永田先生の『多変量解析法入門』も基づく多変量解析は最後となります。ありがとうございました。本書は統計検定1級を目指す方にとっておすすめです。