アクチュアリー数学で有益な本のため過去問での出題歴が多数ある『基本確率 (経済の情報と数理 2)』のメインの部分を解説します。本記事は期待値周辺の話題を扱います。
『基本確率 (経済の情報と数理 2)』に関する記事は4部構成となっています。本記事は第3部になります。
第1部:第1章と第2章(確率の出し方)
第2部:第3章と第4章(ベイズの定理)
第3部:第5章〜第8章(確率分布総論)
第4部:第9章と第10章(条件付き分布と極限理論)
基本確率の第5章の例



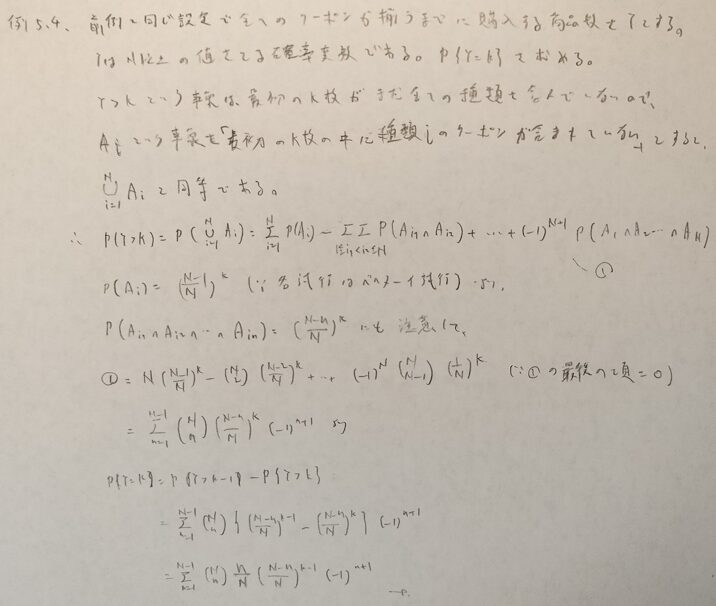
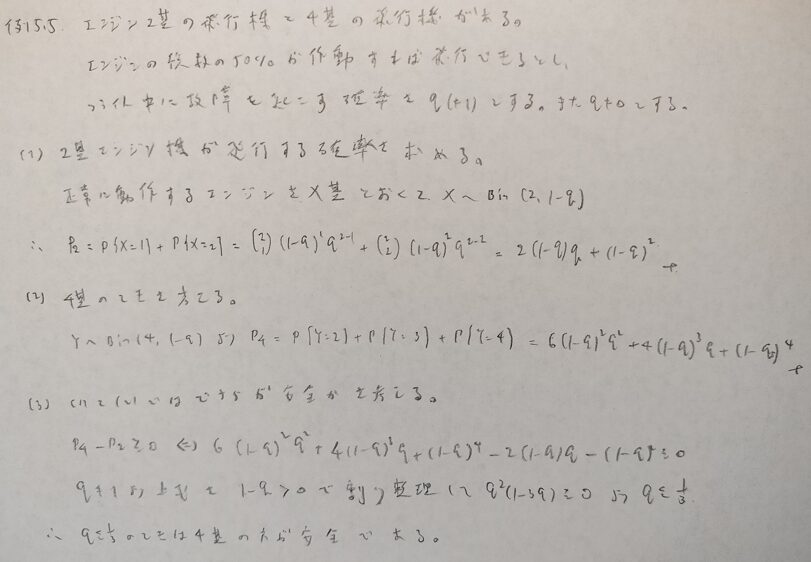
二項分布についてはこちらの記事で詳しく解説しています!
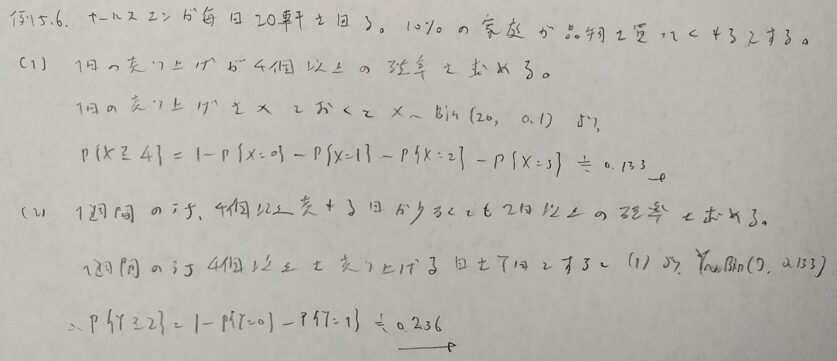
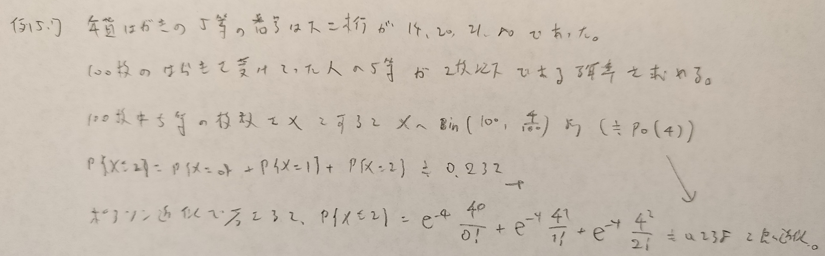
ポアソン分布についてはこちらに詳しい解説があります!
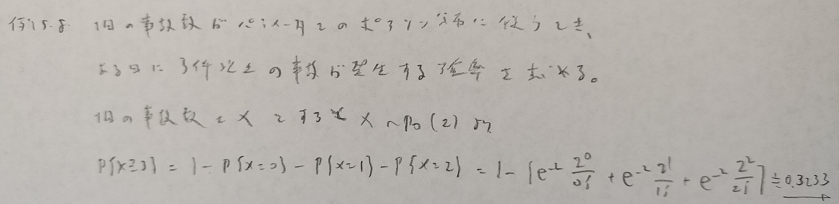
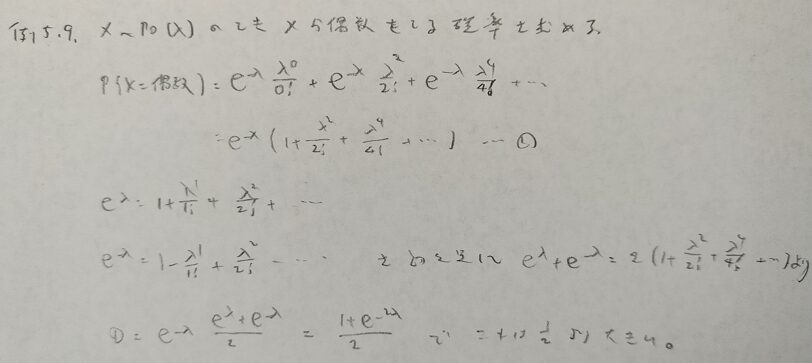
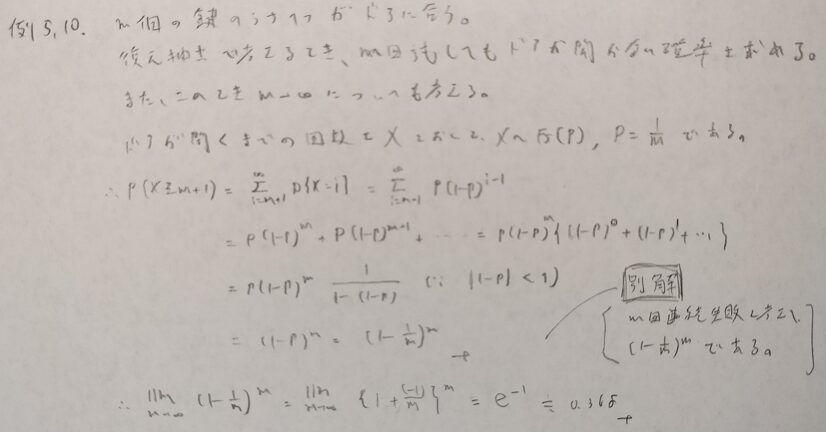
ファーストサクセス分布はこちらに別記事があります!
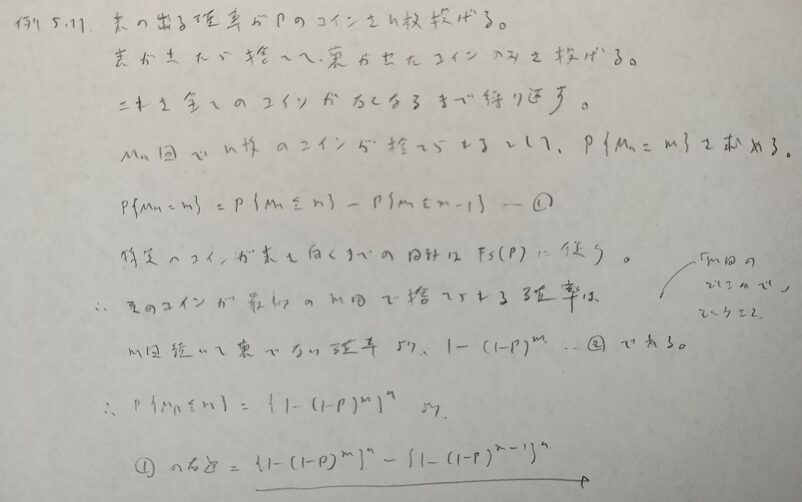
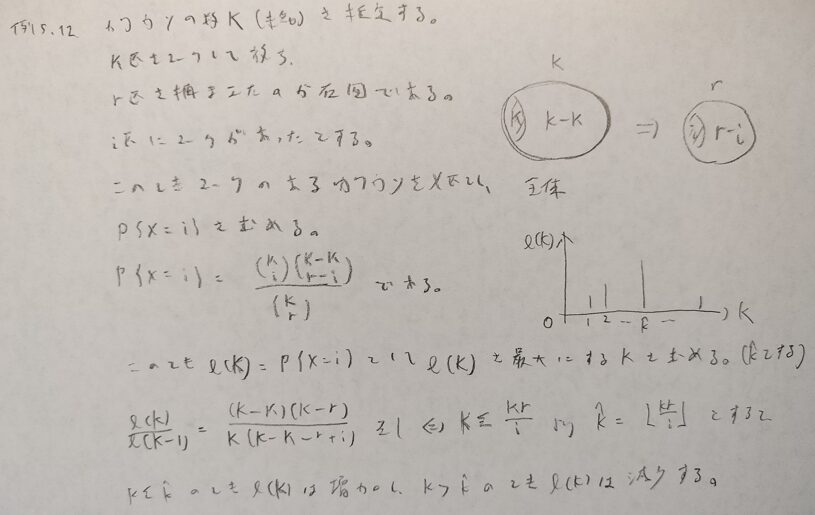
超幾何分布についてはこちらに説明があります!
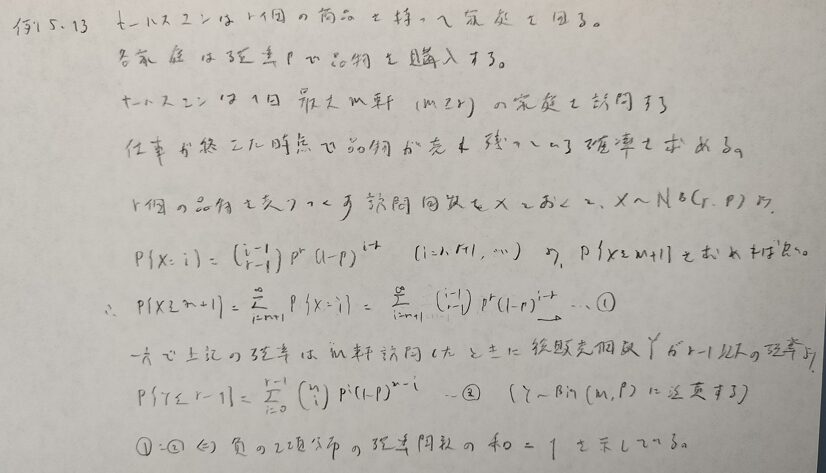
負の二項分布関連はこちらで詳しく説明しています!


基本確率第5章の演習問題
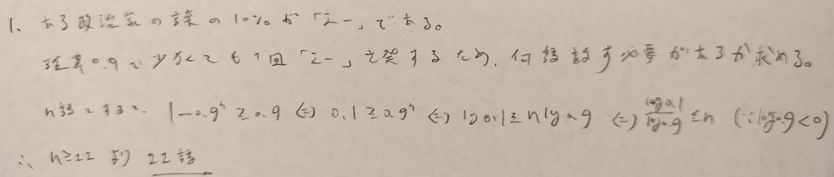
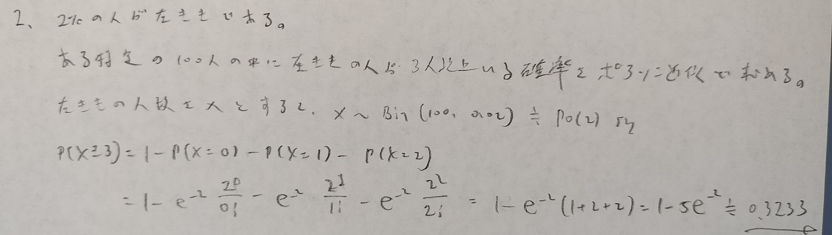





基本確率の第6章の例
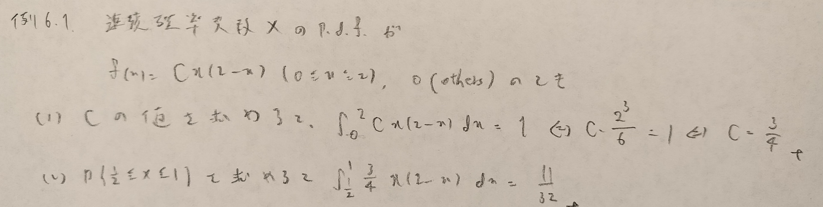

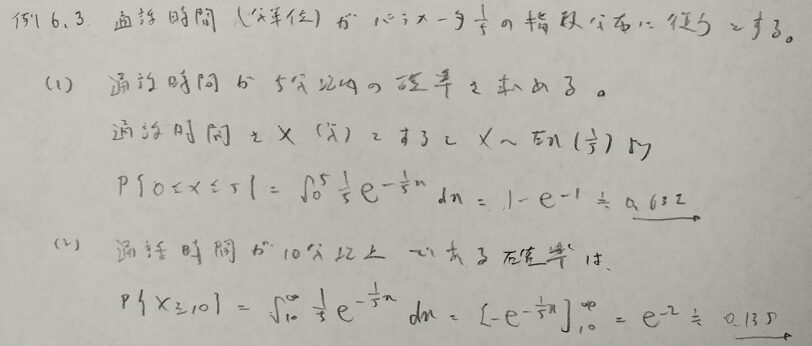
指数分布に関する別記事はこちらです!
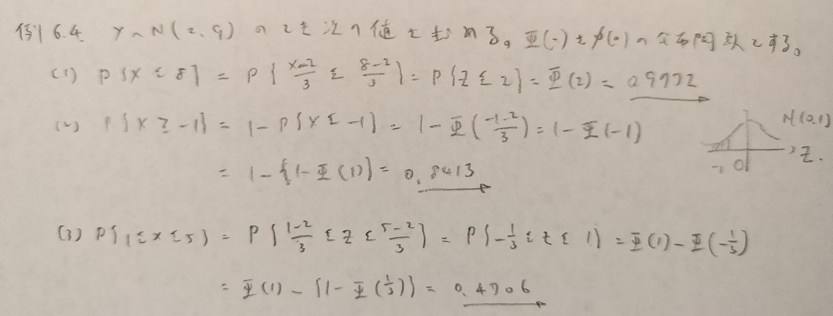

正規分布に関する詳しい説明はこちらです!
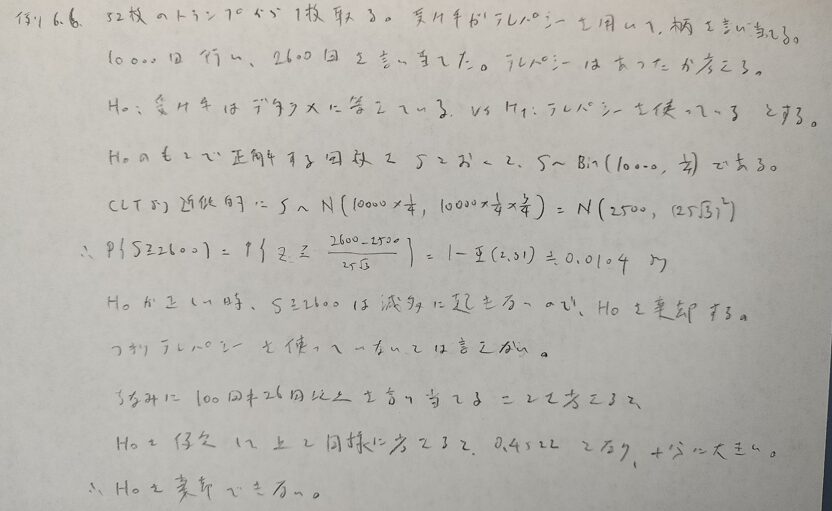
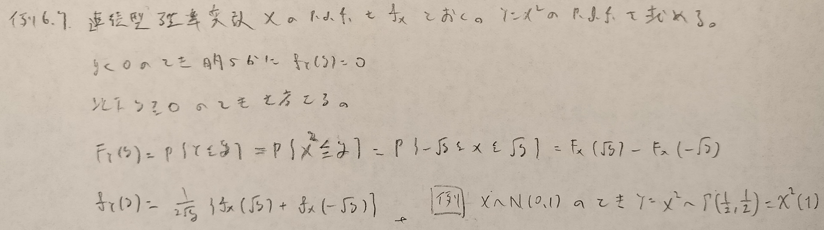
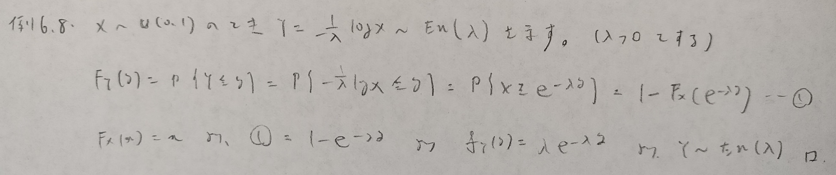
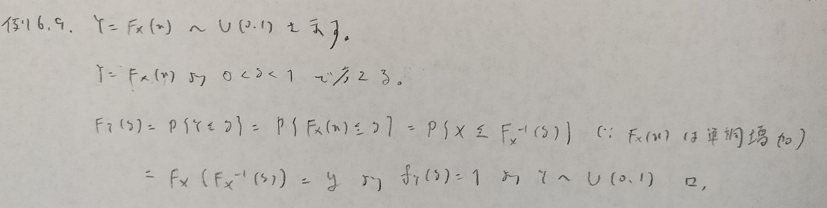
基本確率第6章の演習問題
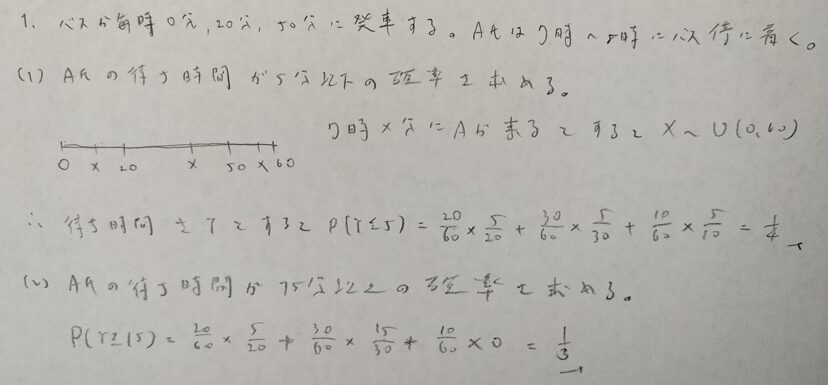
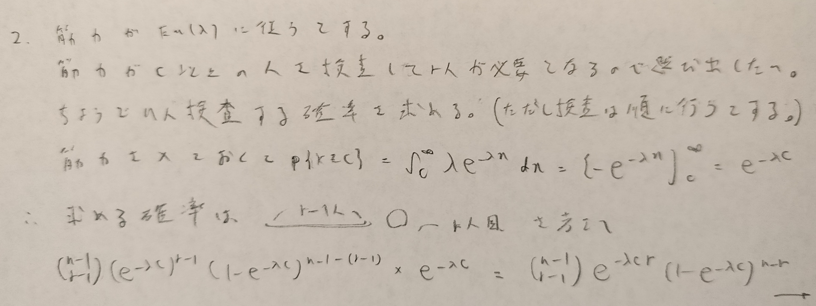

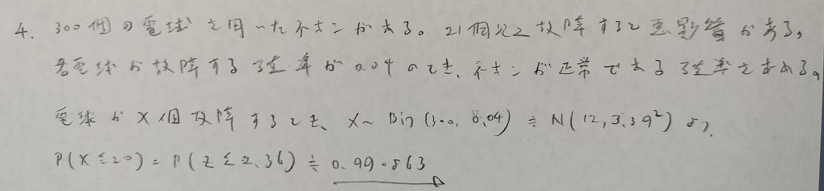
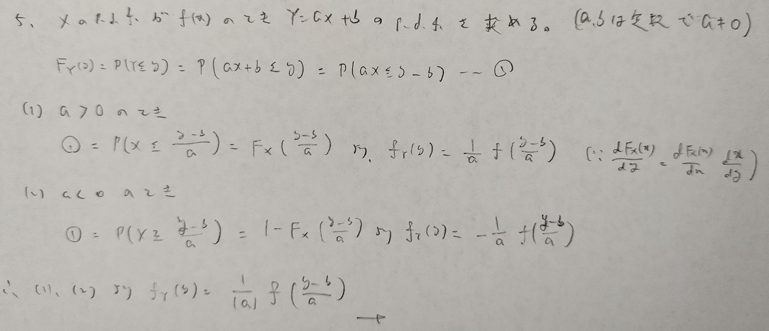
基本確率の第7章の例
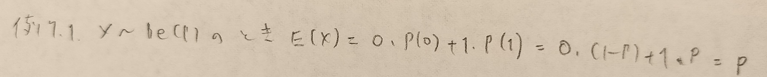
ベルヌーイ分布に関する説明はこちらです!
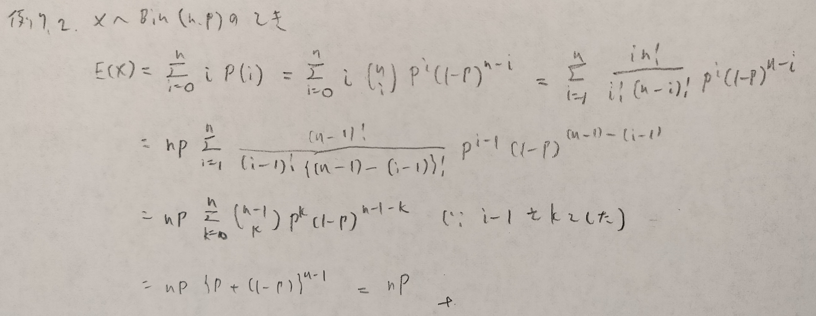
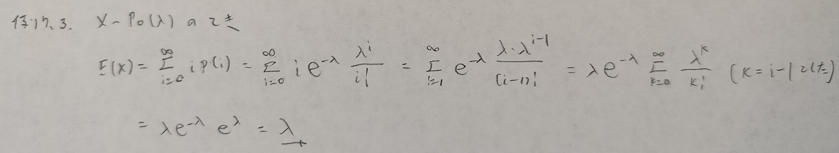
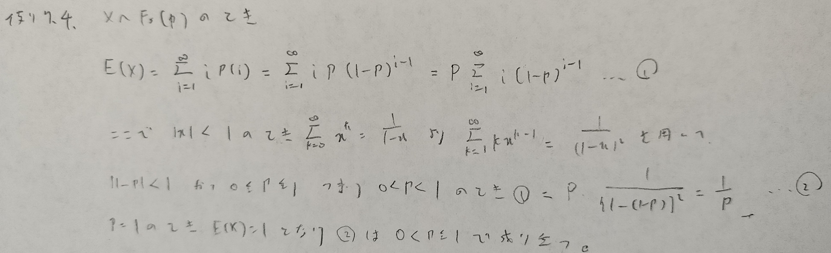
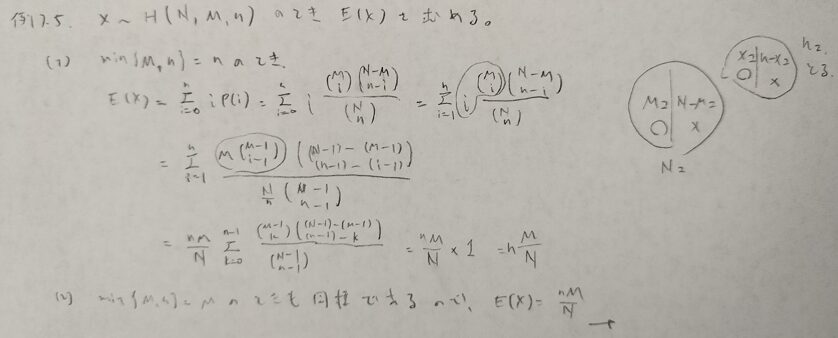
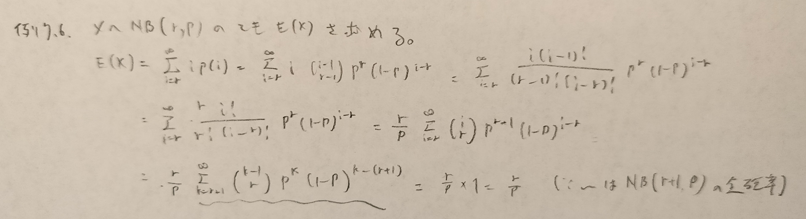

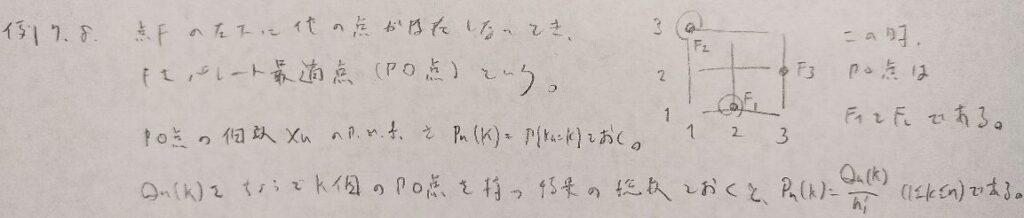
とても難しい問題なので複数に分けます。上の最後の式を☆と置いておきます。

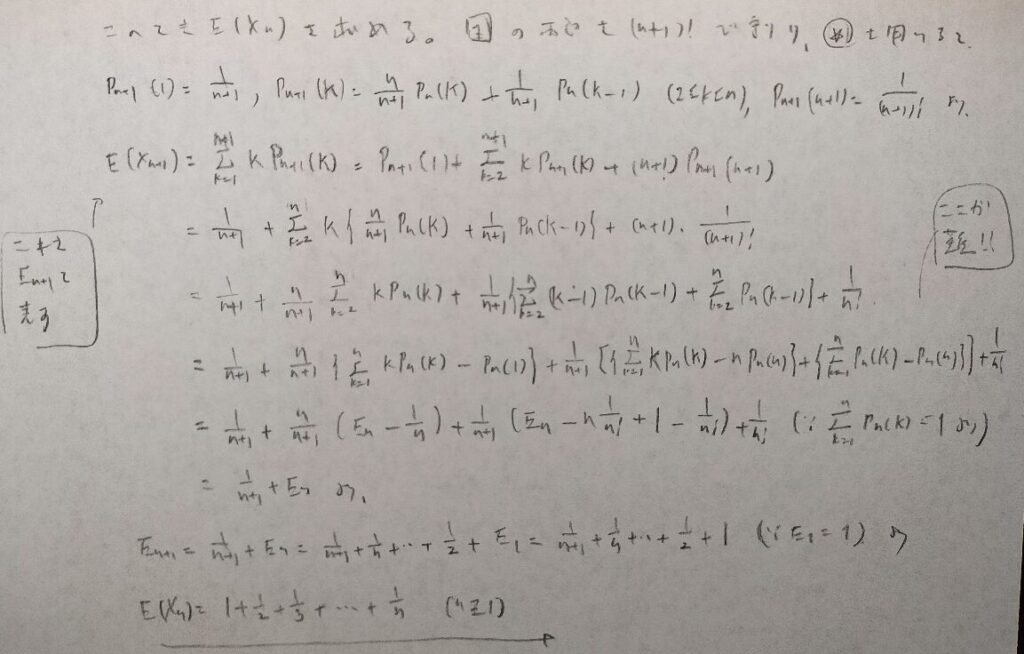
本記事におけるもっとも難しい確率分布です。以降の問題にたびたび登場します。

確率変数Xが非負整数値をとるときに成立する公式です。

期待値がしっぽ確率で表現できるのは不思議です!
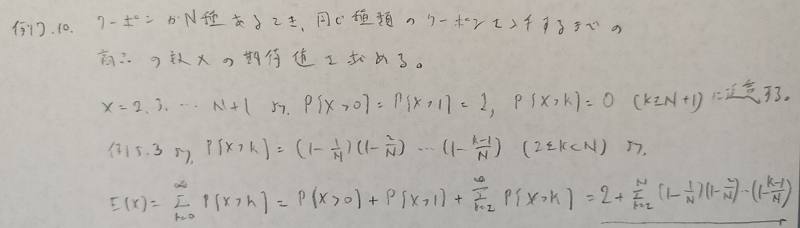
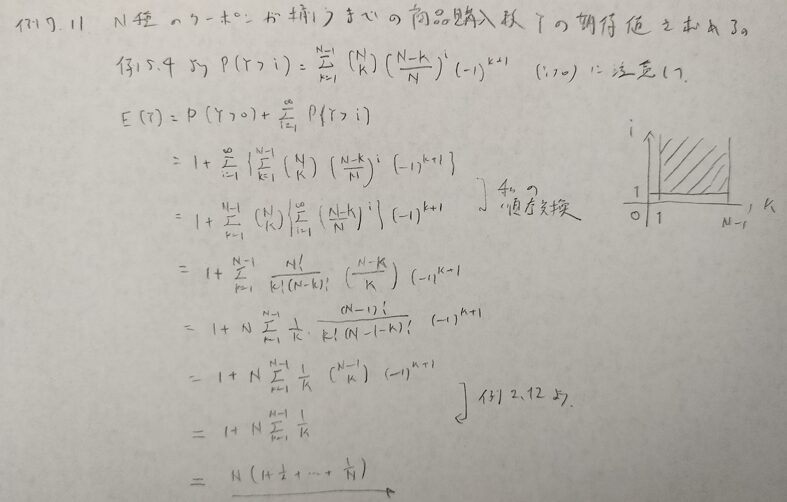
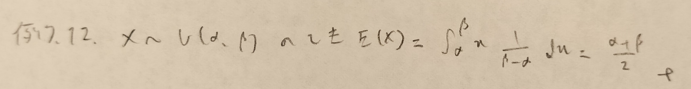
一様分布に関する別記事はこちらです!
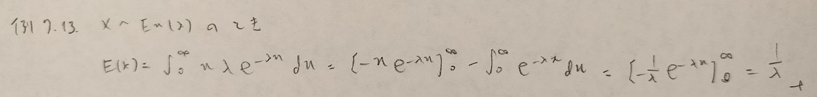
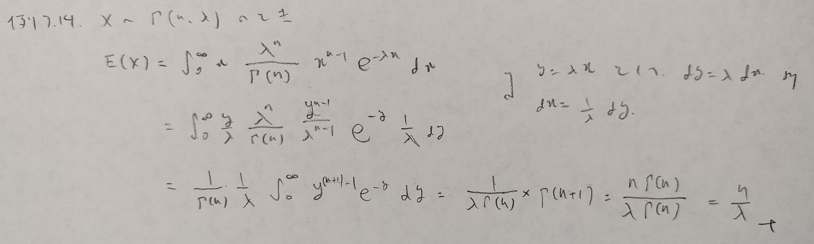
ガンマ分布に関する詳しい説明をこちらでしております。
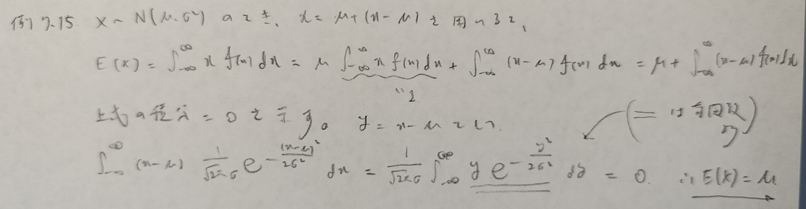
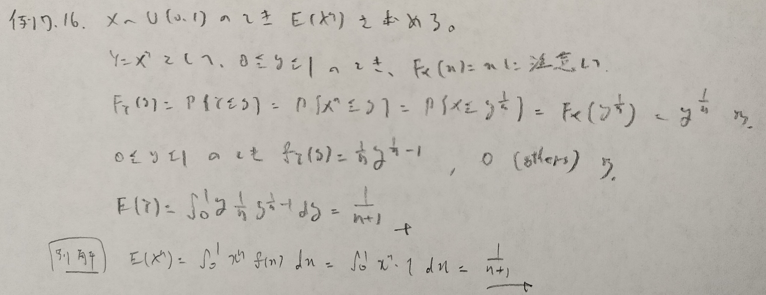

アクチュアリー数学の過去問で大問として出題歴があります。
『基本確率 (経済の情報と数理 2)』を参考にしたことはほぼ間違いないですね!笑
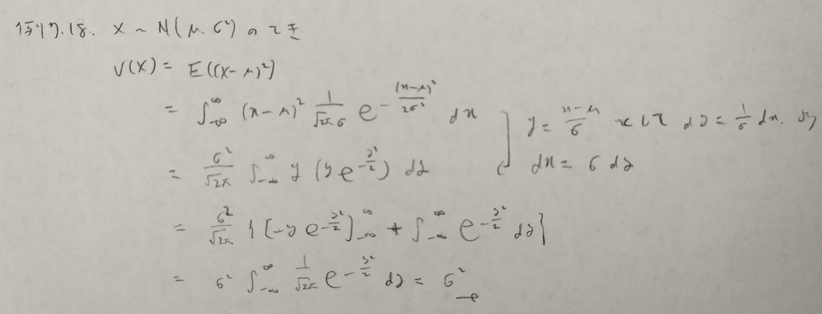
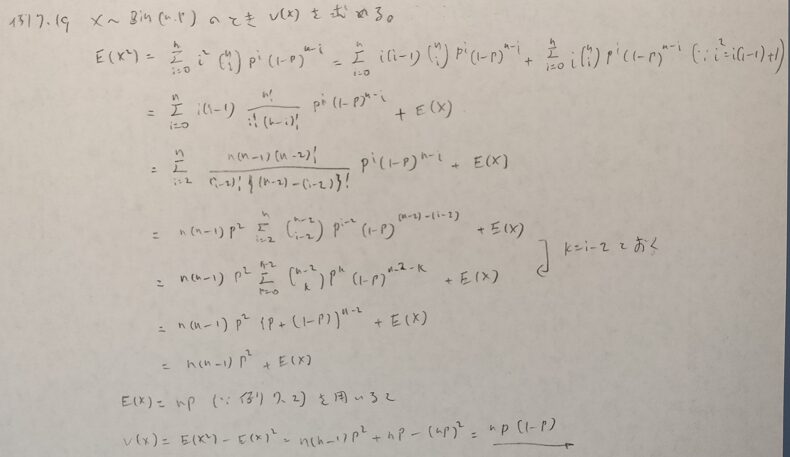
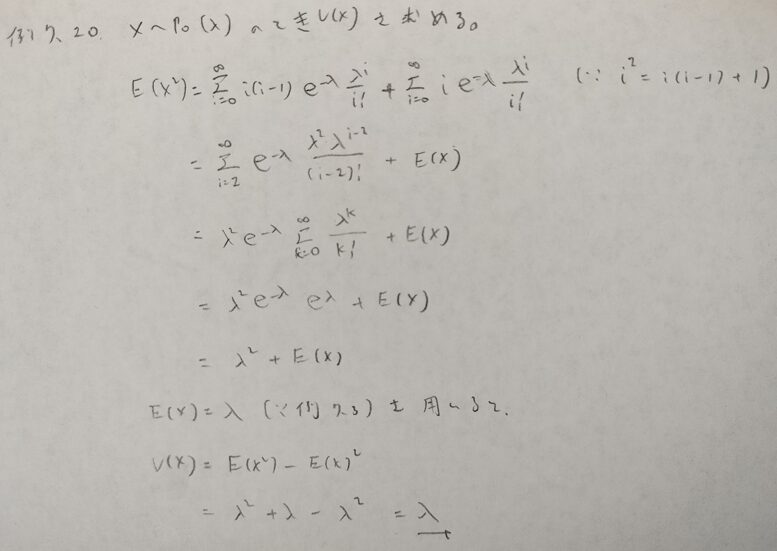
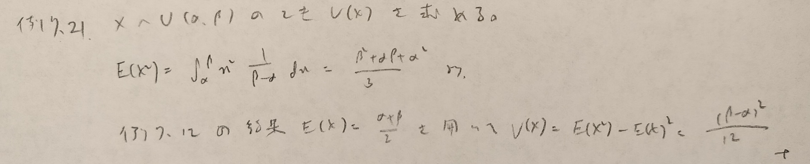
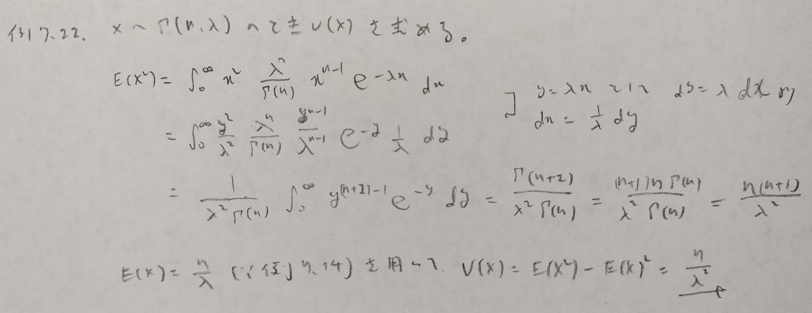
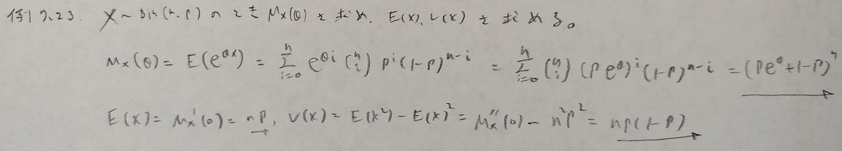
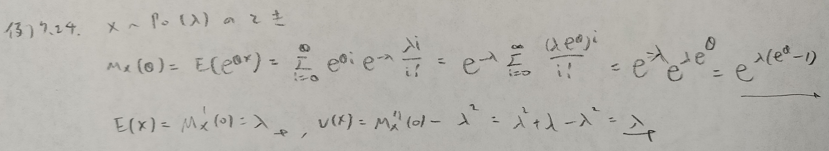
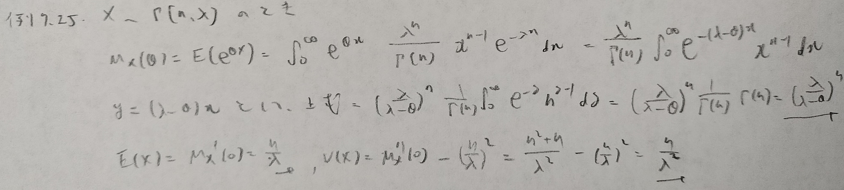
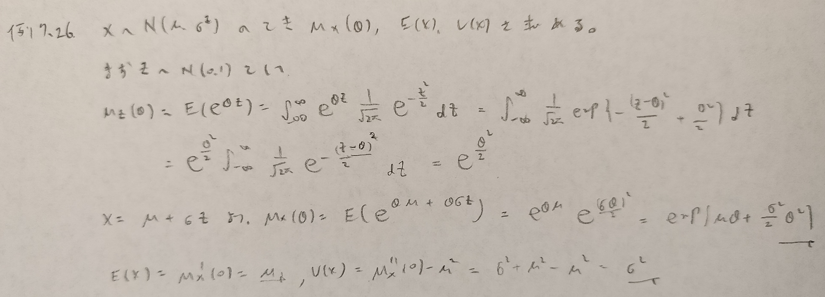
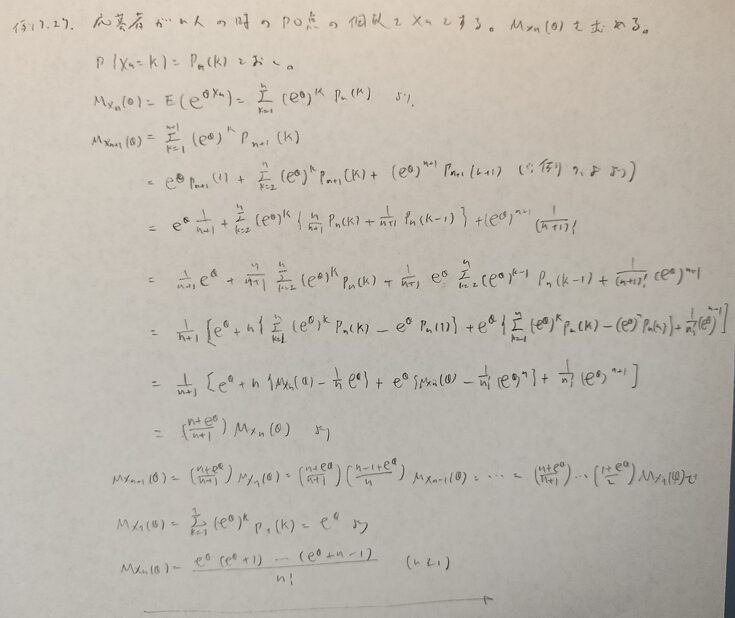
基本確率第7章の演習問題
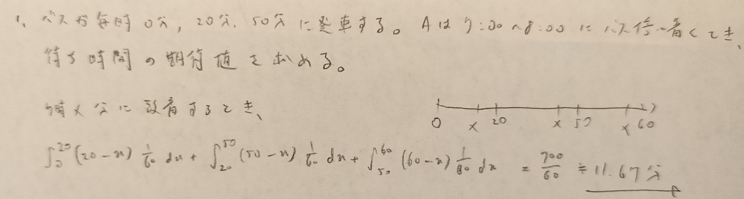

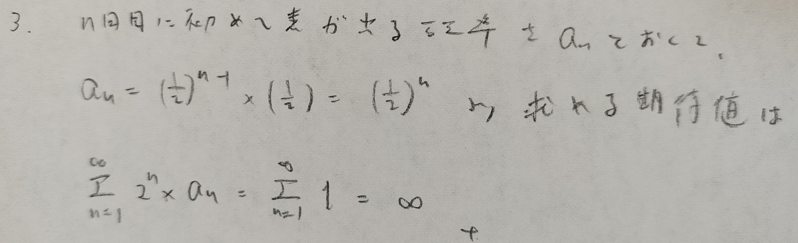
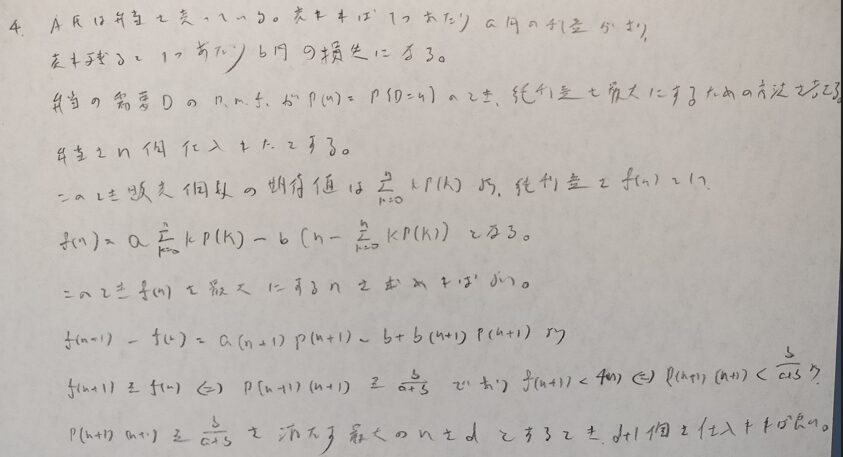
何問です。当事者からみた期待値の金額について考えて立式しました。
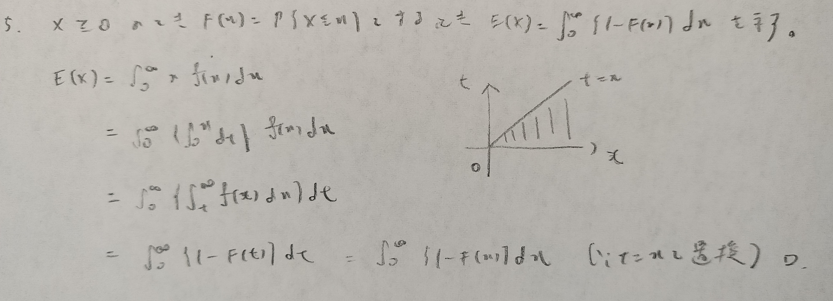
確率変数Xが非負なのは離散バージョンのタイプと共通事項ですね。
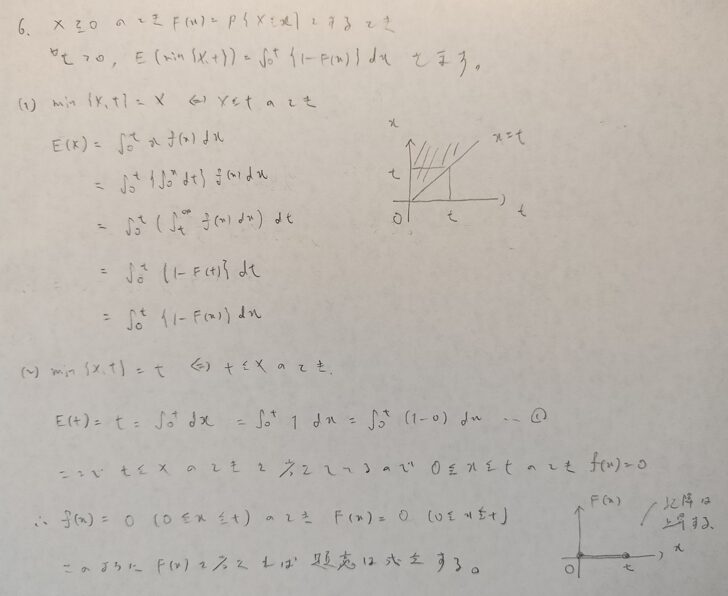
とても難しい問題です。(1)の式変形は結論部分の式から辿っていくことによって道筋が見えました。

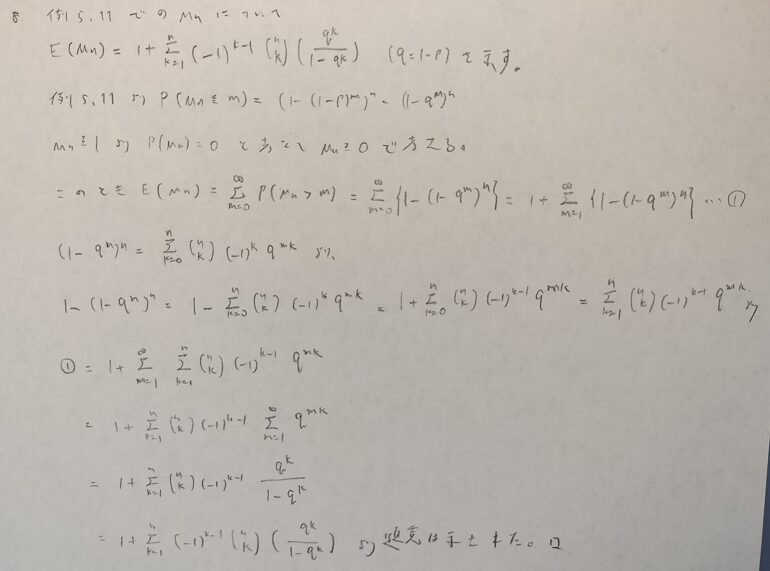
基本確率の第8章の例

結合「確率分布」関数で意味が切れます。
分布関数と書いてるので「あれ」と思いました。
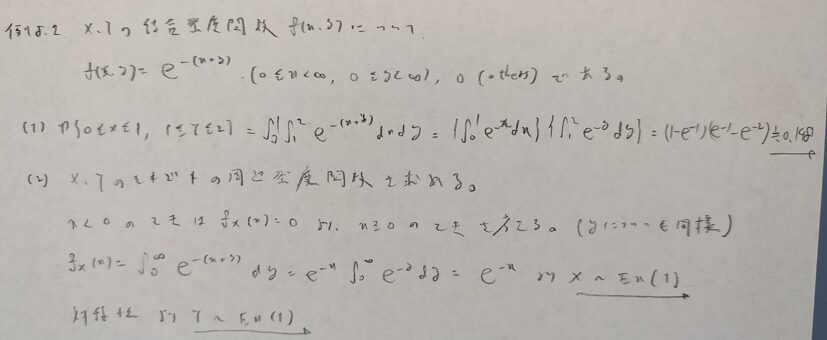
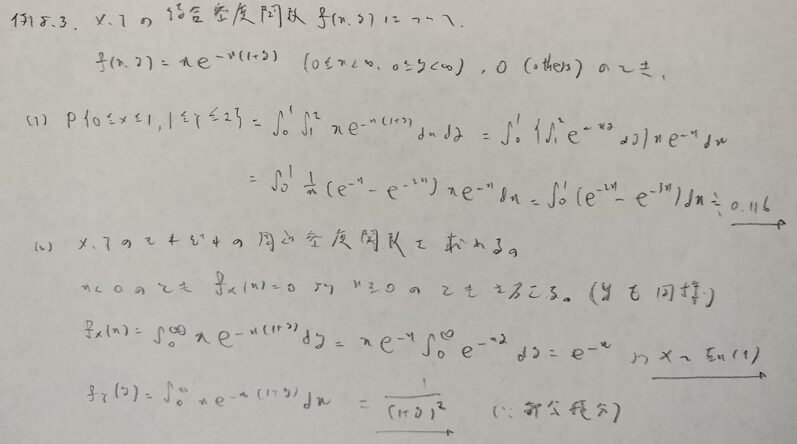
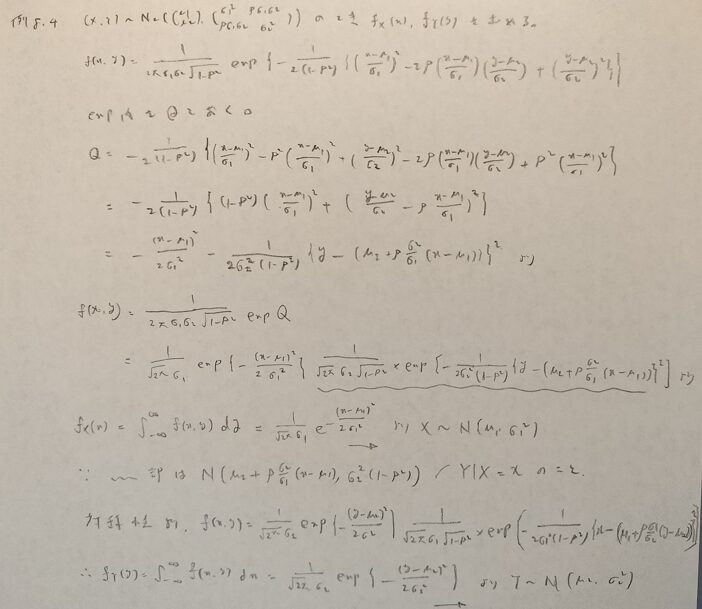
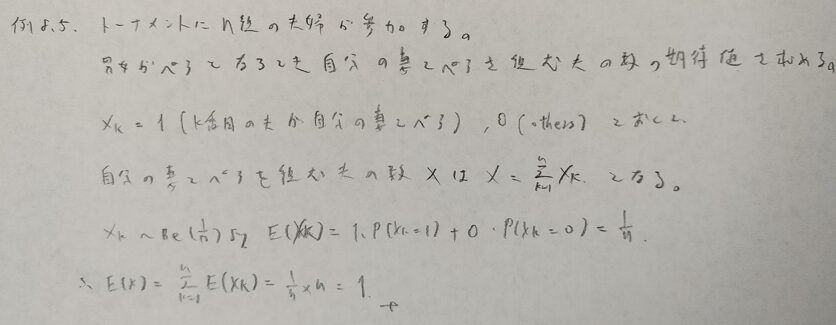
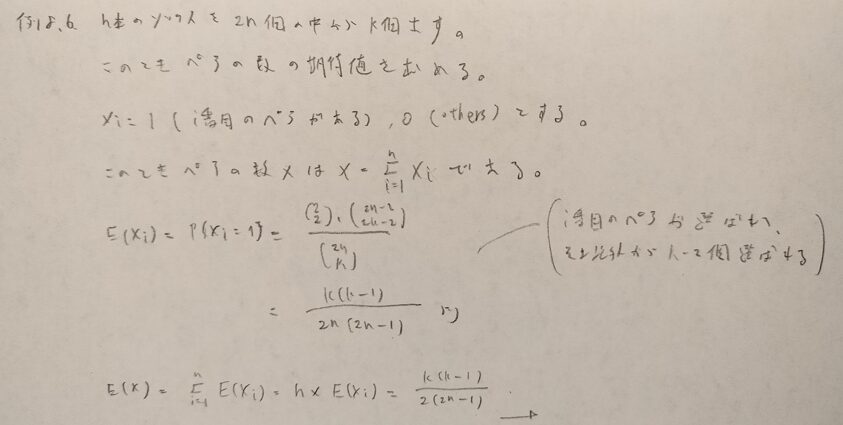
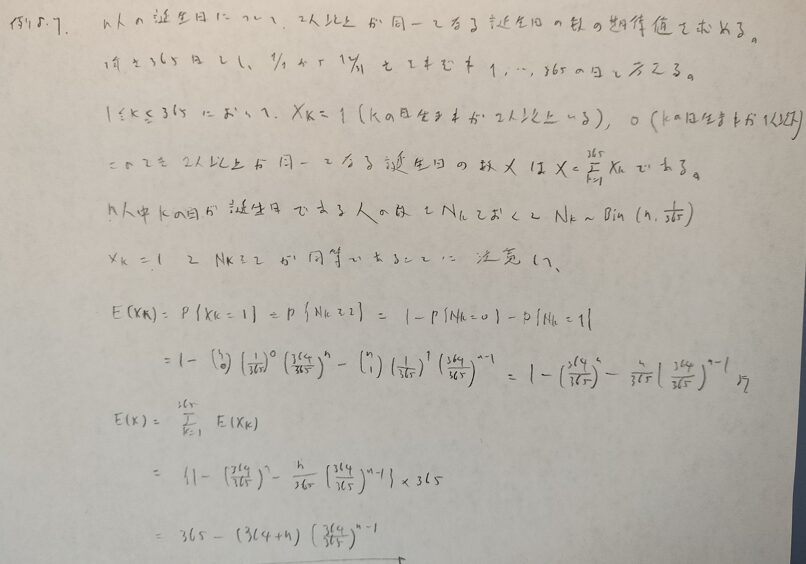
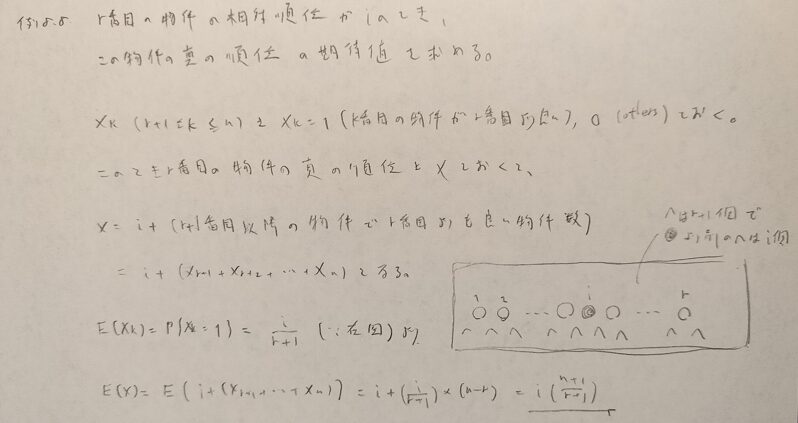

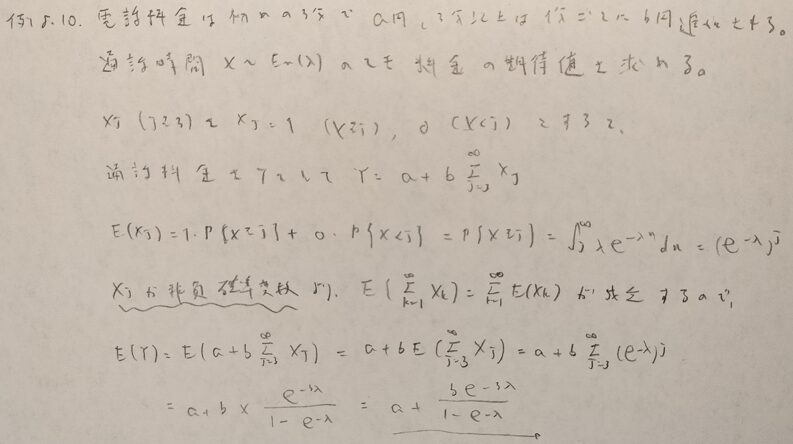
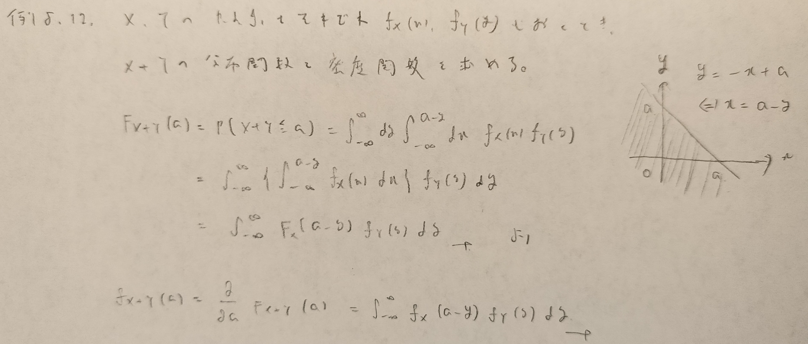
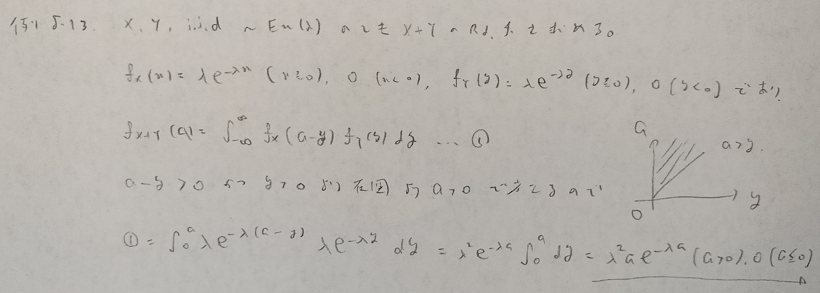

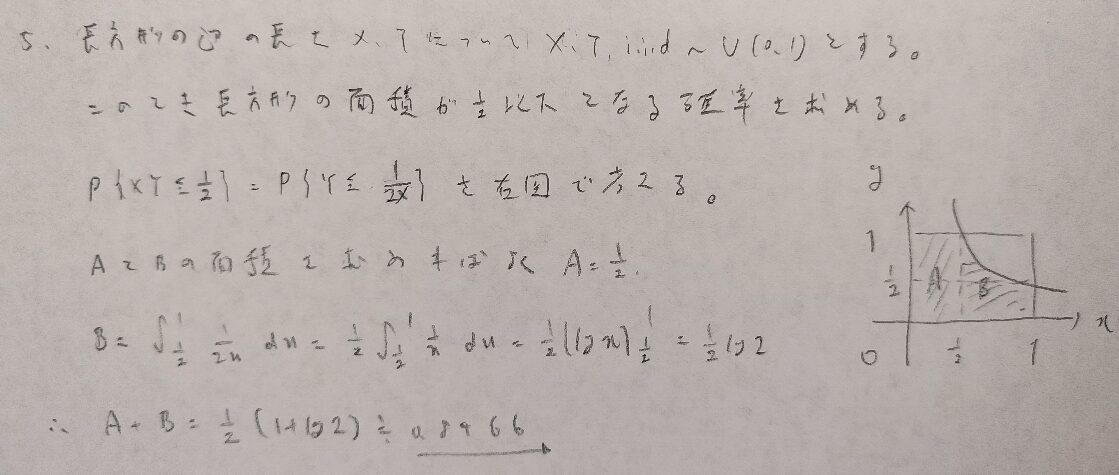
アクチュアリー数学でまったく同じ問題が出題されています。
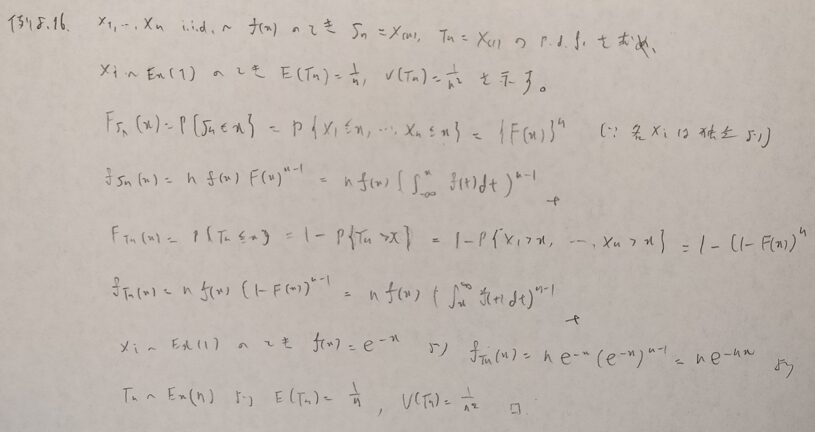

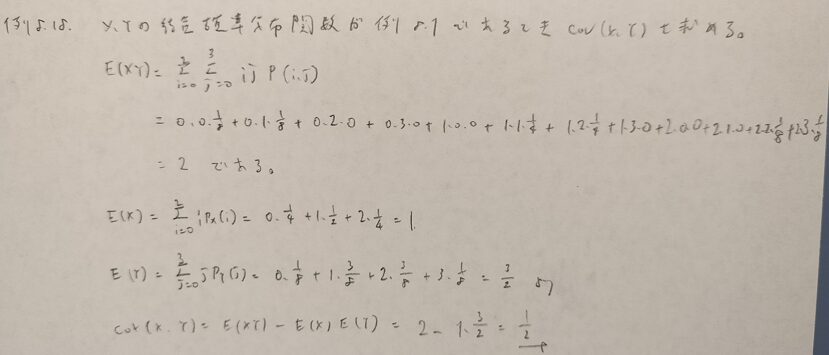
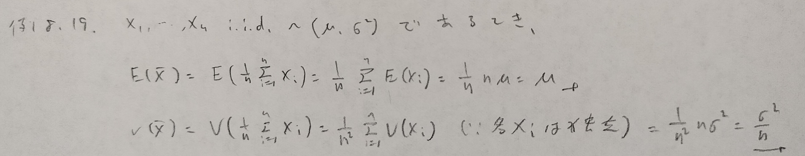

パラメータ1の指数分布を考える際は、本問の結果に意味を持たせることができます。
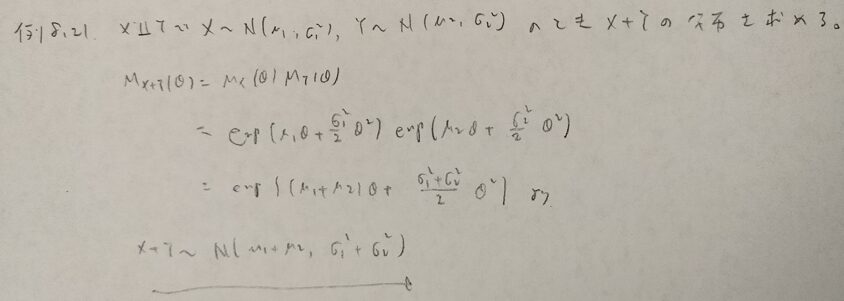
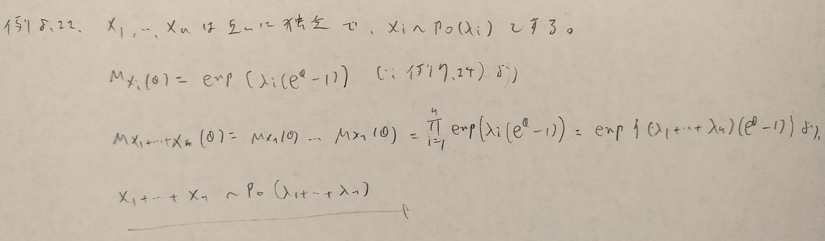
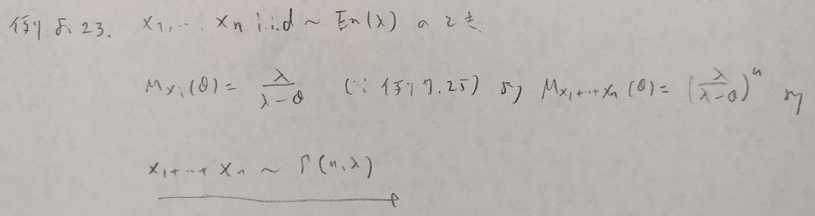
基本確率第8章の演習問題
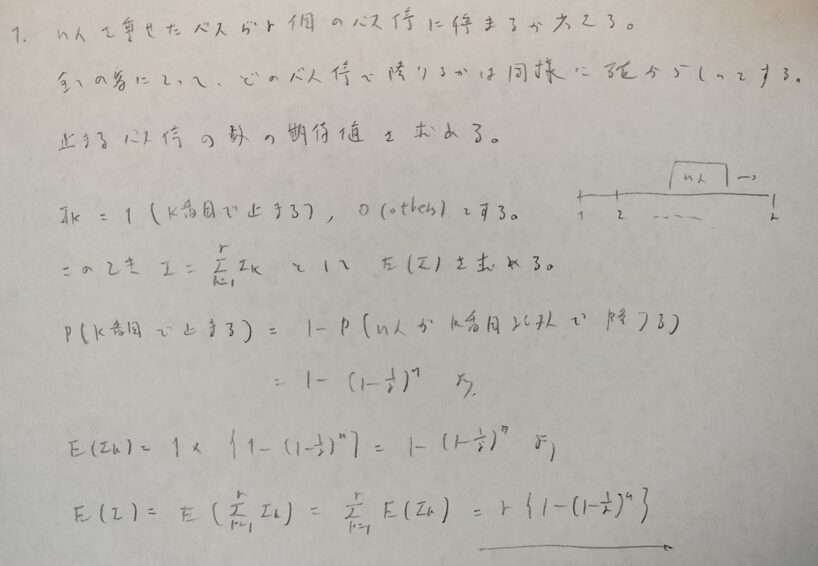
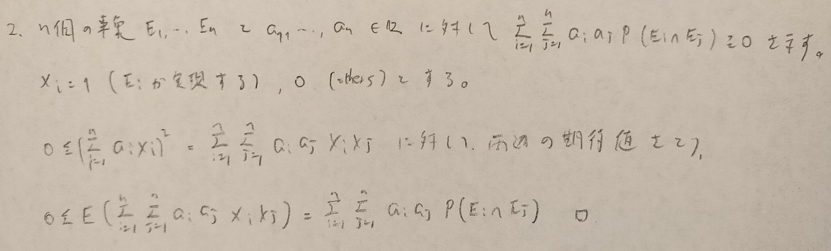
初見では難しい問題です。本章でたびたび登場する確率変数の分解の考え方を用います。

確率変数をどのように分解するのかが難しく感じました。
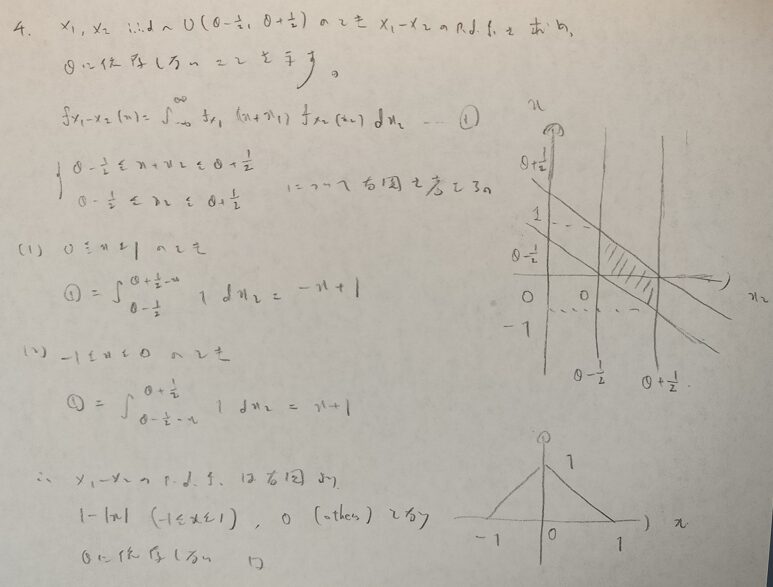
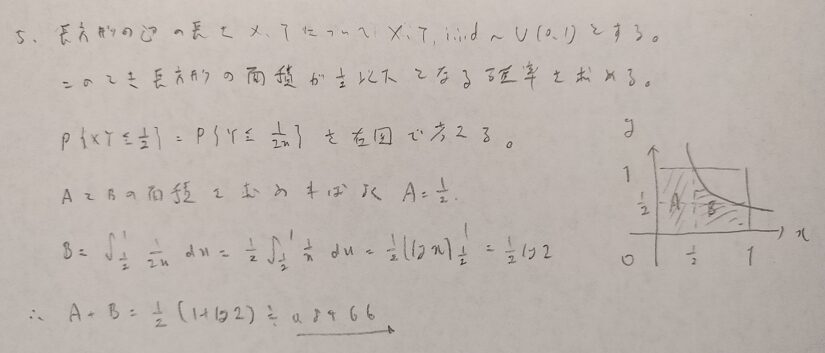

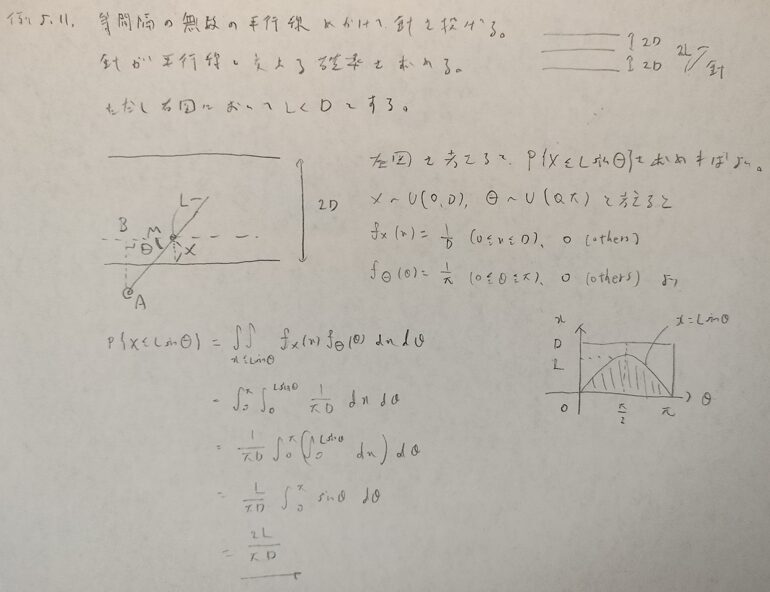
答えが50%だと思っていたので結構、驚いています!
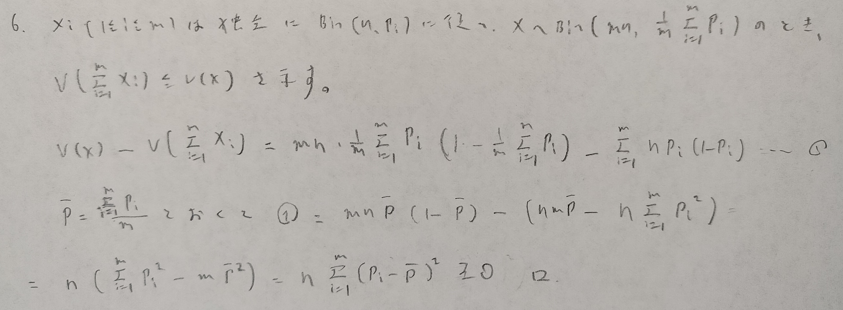
かなり込み入った設定です。最後の式は分散の公式を連想できれば通過できます!
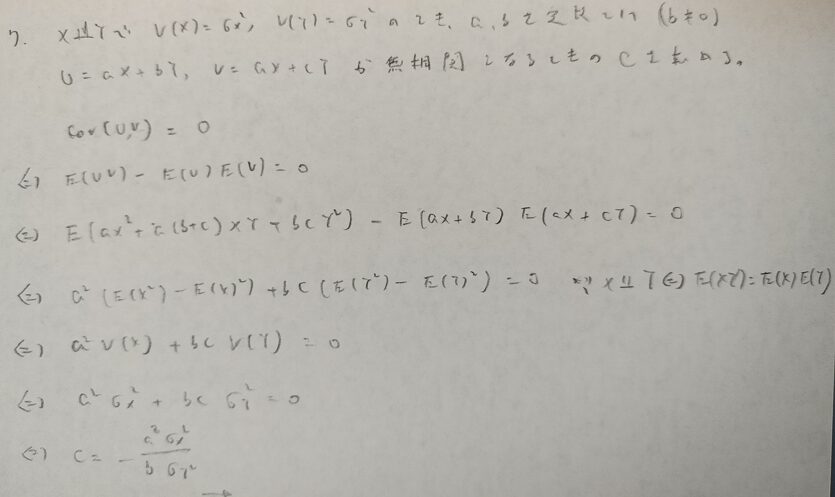
今回は『基本確率 (経済の情報と数理 2)』のメインの部分となる期待値周辺の話題を解説しました。ところどころ実生活に使えそうな問題があったとは思いませんか?
待ち時間の問題とか面白かったです。でも私的には面積が0.5以下になる確率を求める問題で高すぎる結果となったことに衝撃を受けました。次回の第4部も楽しみにしています!
『基本確率 (経済の情報と数理 2)』はアクチュアリー数学対策としても確率の読み物としても素晴らしい本です。本書を片手に次回も一緒に頑張りましょう!