アクチュアリーの主に確率分野の対策として過去問の的中率が高い『基本確率 (経済の情報と数理 2) 』に関する記事の第２部です。第１部はこちらです。
本書に関する記事は全部で４部構成となっていますので、今回までで本書の半分を終えたことになります。
第１部：第１章と第２章（確率の出し方）
第２部：第３章と第４章（ベイズの定理）
第３部：第５章〜第８章（確率分布総論）
第４部：第９章と第１０章（条件付き分布と極限理論）
本記事では第４章の例題に難問が集中しています。しかし最後の答えの結論について考えさせられる問題が多く、どの問題も見逃せません！
基本確率の第３章の例
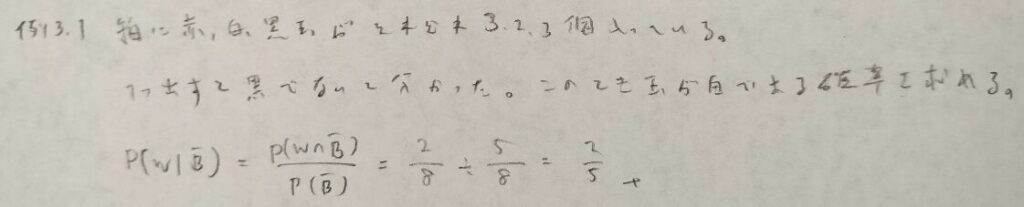
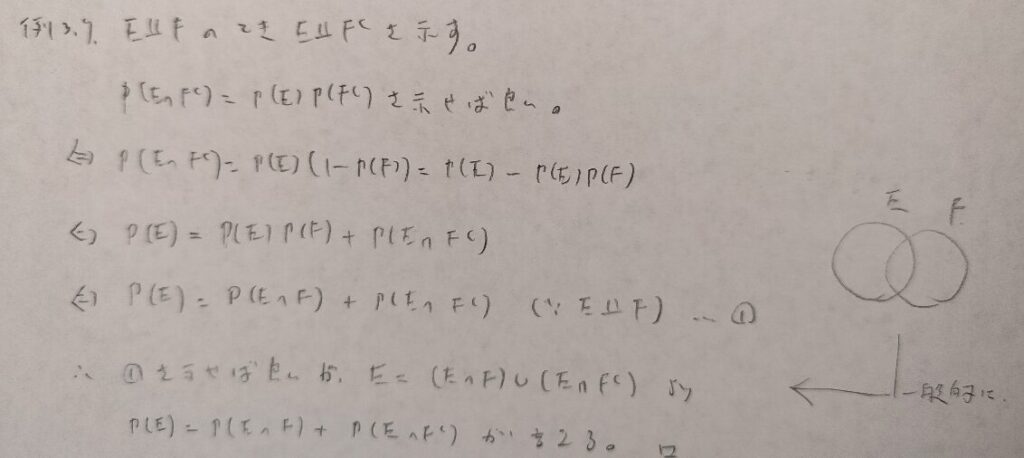
第３章や第４章のこのような証明問題は結論を同値変形していくと示すべき式が見つけやすくなります。
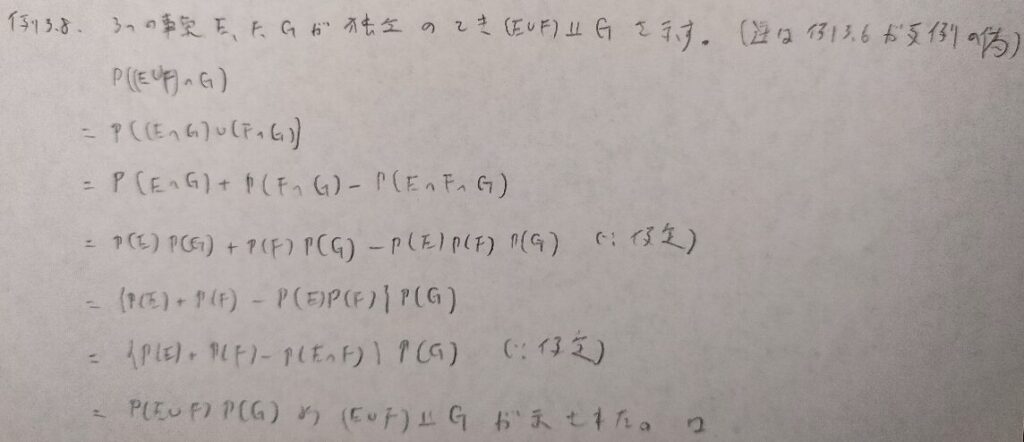
ペアワイズ独立とは『データ解析のための数理統計入門』に詳しく載っています。統計検定では準１級のレベルです。３つ以上の事象が独立とは任意の２つの事象が独立（２つの積事象の確率が２つの事象の確率の積に分解できる）、かつ３つの積事象の確率が３つの事象の確率の積に分解できることが必要十分で一般化可能です。
より詳しい説明はアクチュアリー数学対策として有名な通称リスク本『リスクを知るための確率・統計入門』に丁寧に載っています。
とても意外な結果でした。私は（２）の方が有利だと思っていました。確率は面白いですね！
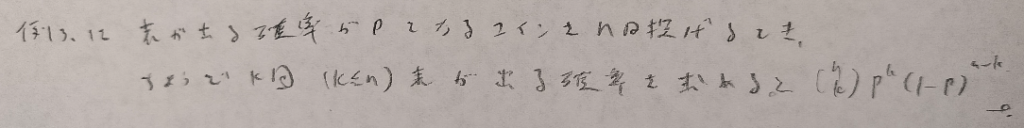
第３章での唯一の難問です。この結果は紳士的ではないと思われるかも知れませんが生き残るためには有効な手段です。
基本確率第３章の演習問題
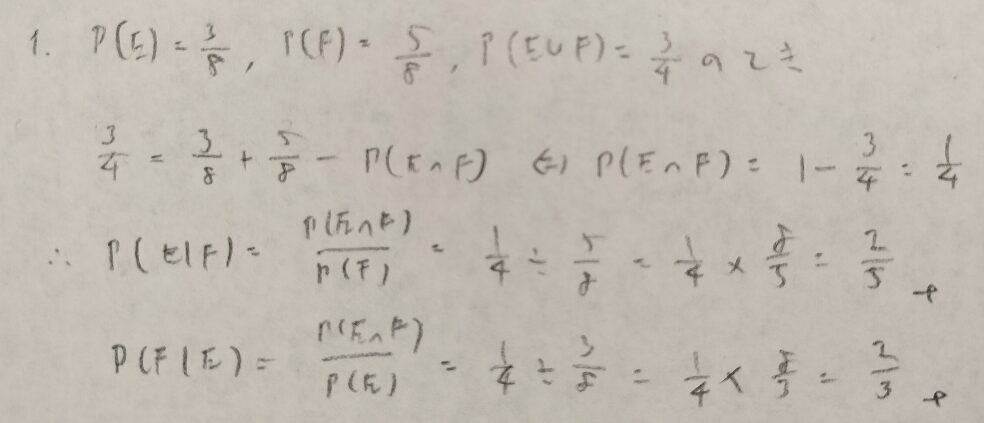
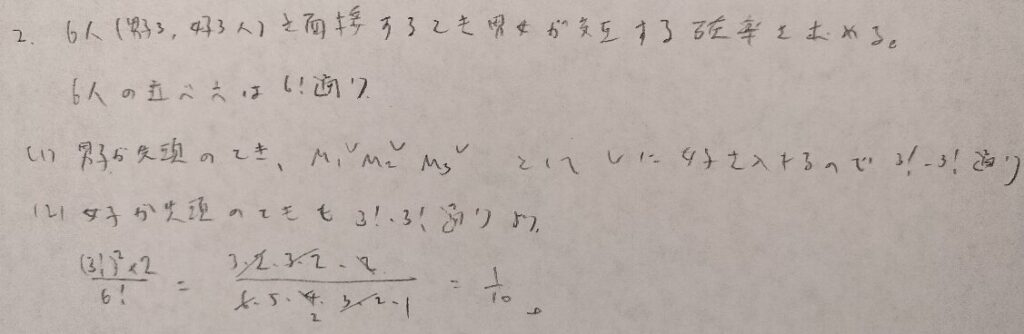
事象をどのように設定するかで解けるかどうか別れる難問です。
基本確率の第４章の例
第４章はこれまでの章とは異なり例題の多くが難問です。
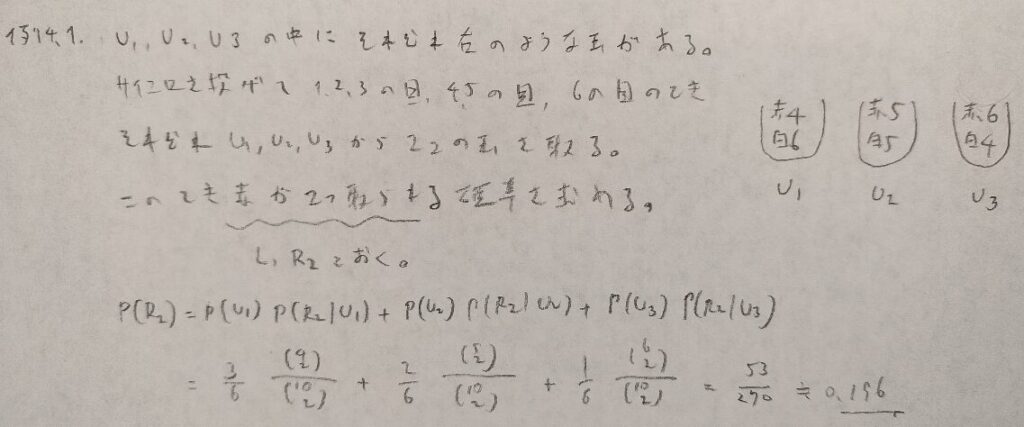
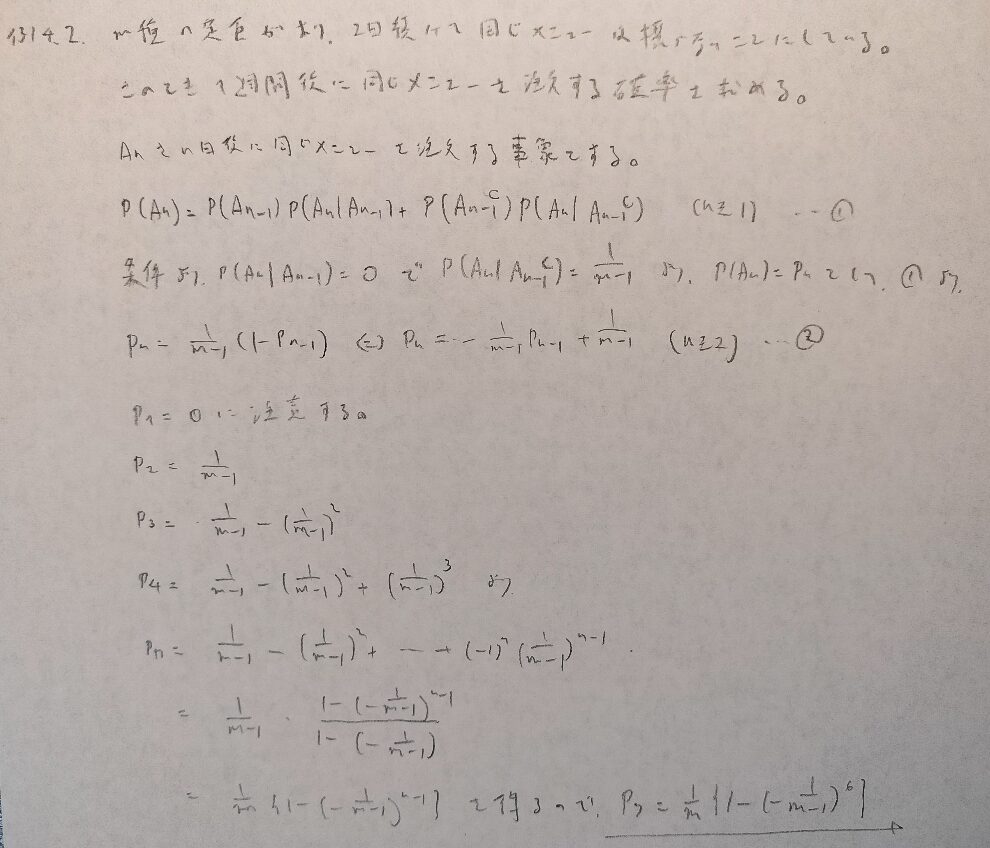
アクチュアリー数学の過去問でほぼ同じ問題が出題されています。
巴戦で実力が拮抗している場合は対戦順で有利不利が出てきます。
これは初見ではみんな引っかかる問題ですね！
僕は初めてこの事実を知った時は衝撃でした。確率の問題を解いていて最も衝撃が走った問題でした。
難問です。初見ではまず解けないでしょう。アクチュアリーの試験形式的に、どのような出され方で問われても正解したい問題です。
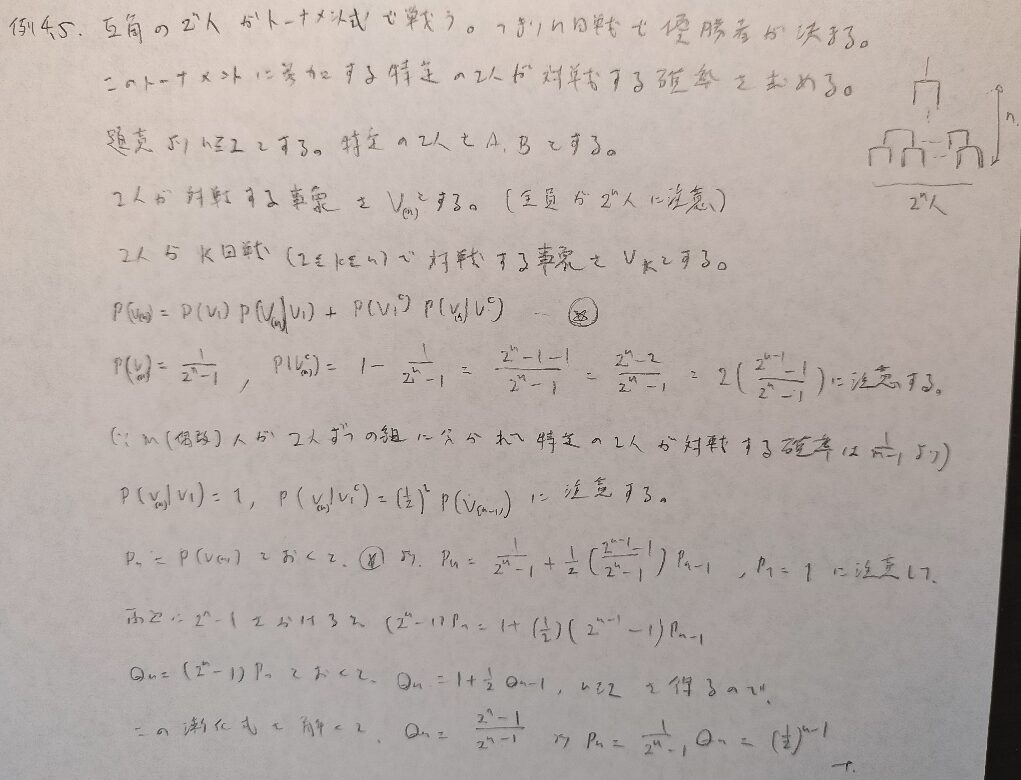
難問です。難問ですが実用的な問題です。
超有名問題です。結果は暗記したいですね。
難問です。そもそも破産の確率（先に実現してしまう確率）を使おうと思うところから難しいです。
ほぼ確実に犯人の人を「あなたは犯人じゃない」と無罪の証拠を集める努力がとても切ない行動に感じる良問です。
コナン君の名セリフが蘇ります。
モンモールの問題は2023年度の統計検定１級の統計応用の共通問題で出題されました。
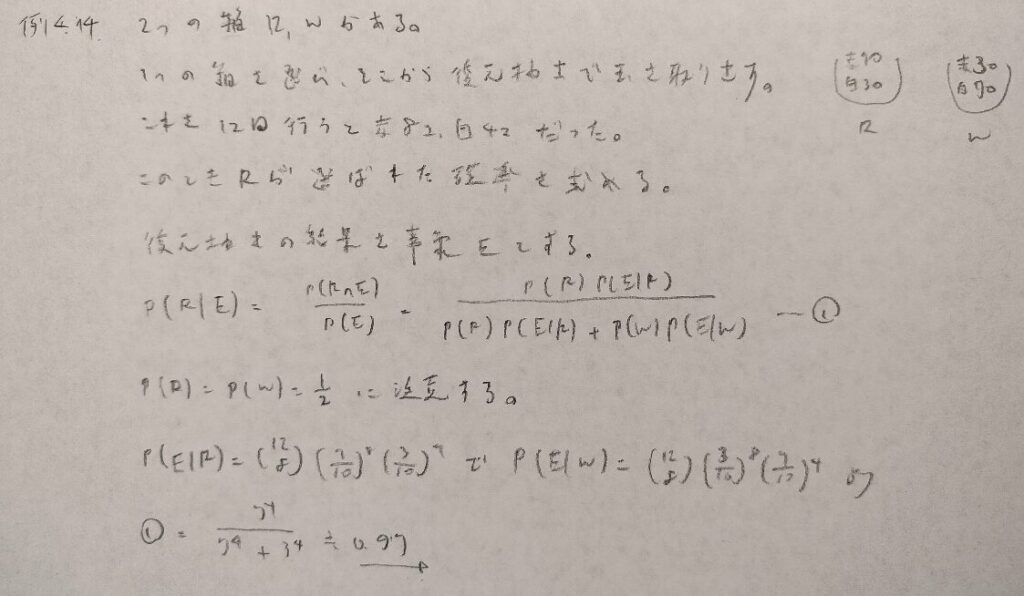
基本確率第４章の演習問題
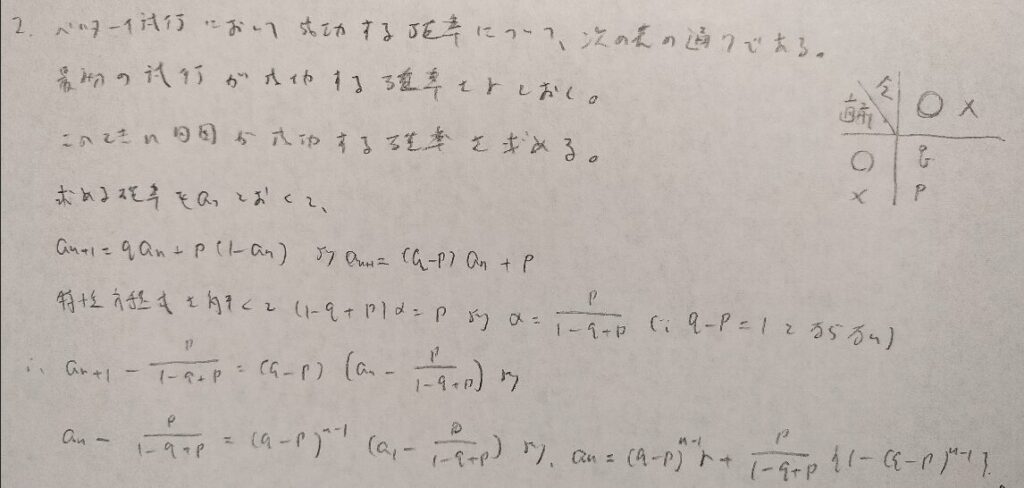
第４章の演習問題での難問です。とにかく事象の設定が難しいです。
第４章は以上になります。特に例の後半あたりの難問が厳しかったですね。
難しかったですが結果に驚く問題が多くて楽しかったです。
次回も『基本確率 (経済の情報と数理 2) 』を片手に頑張りましょう！
 』に関する記事の第２部です。第１部はこちらです。 本書に関する記事は全部で４部構成となってい){kind=link}