アクチュアリー数学で出題頻度が高い『基本確率 (経済の情報と数理 2)』の各章の解説の最終部になります。
この記事は第４部になります。第１部かのリンクをまとめておきますので、是非とも辿ってくださいね！
第１部：第１章と第２章（確率の出し方）
第２部：第３章と第４章（ベイズの定理）
第３部：第５章〜第８章（確率分布総論）
第４部：第９章と第１０章（条件付き分布と極限理論）
この記事では第９章の条件付分布がメインです。本章は『基本確率 (経済の情報と数理 2)』の集大成的な内容で特に後半の例の難易度が高いです。
アクチュアリー数学試験で、いまだに出題されていない問題もあります。他の章も未出問題がありますので、詳しい内容は本書をご参照ください。また第１０章ではスターリングの公式を中心極限定理を用いて鮮やかに証明する内容があります。こちらも必見です！
基本確率の第９章の例
本章の前半部は統計検定１級対策の名著『現代数理統計学の基礎』にあるガンマ・ポアソン分布などの例をたくさん集めたものになります。そのため統計検定１級対策にも有効な章になります。
ポチップ
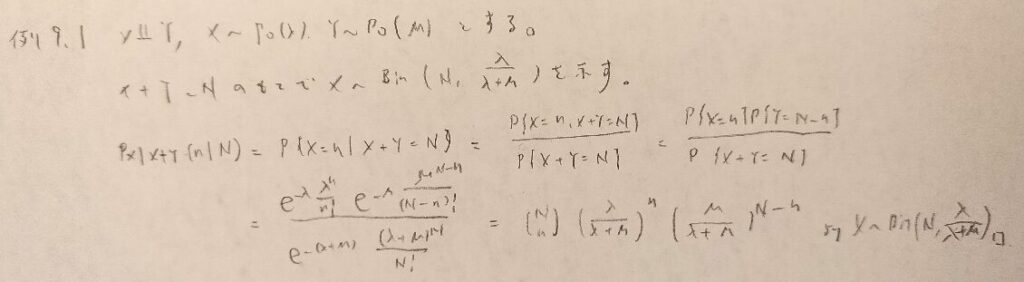
統計検定準１級（合格方法はこちら）でよく登場するベータ・二項モデル（ベータ二項分布）などはパラメータが従う（事前分布）にベータ分布を、条件付き分布に二項分布を用いたXの周辺分布のことを指します。第９章ではこの呼び方のアレンジをして問題を特徴づけていきます。
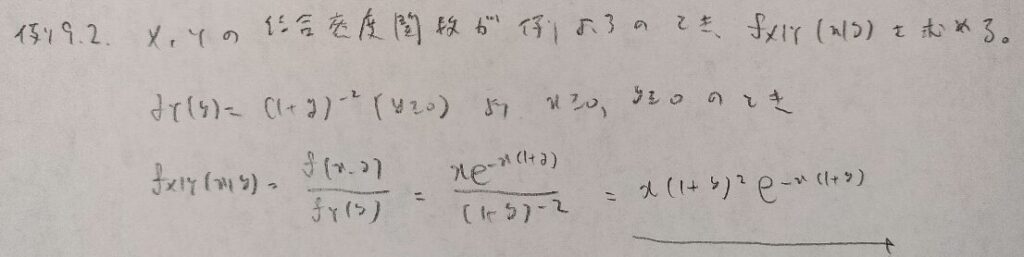
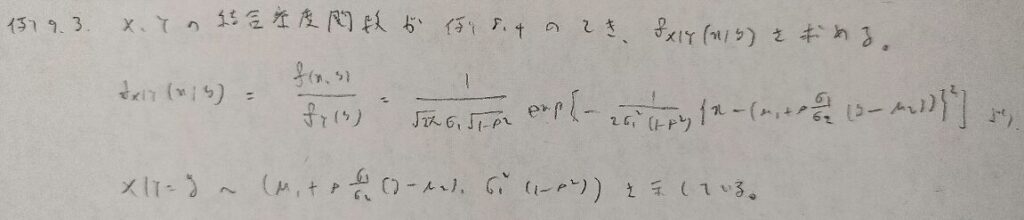
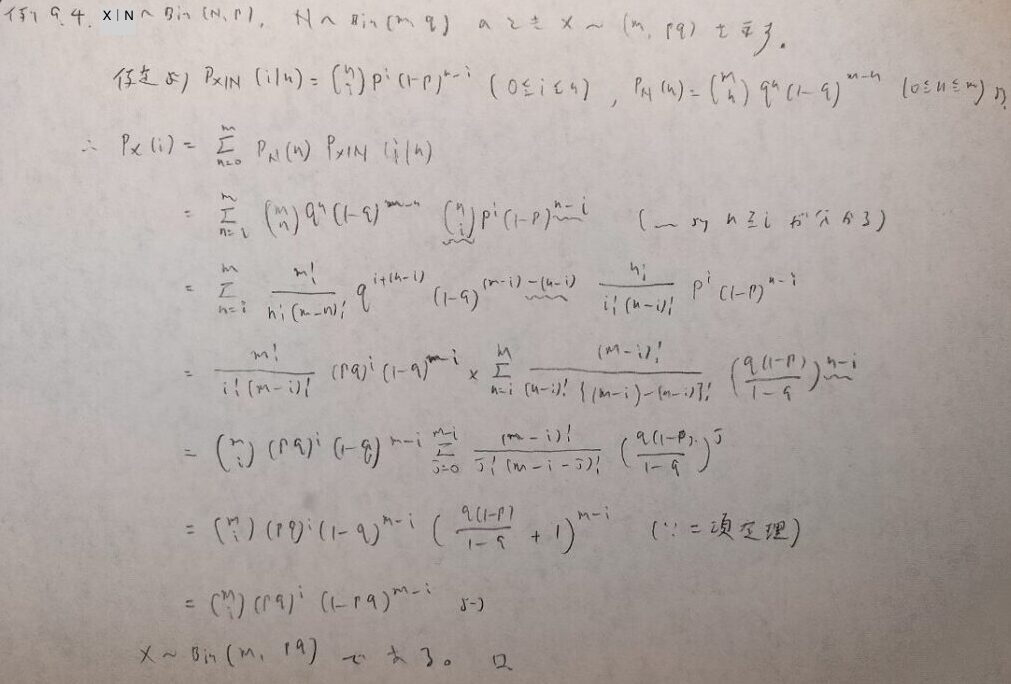
これは二項・二項分布とでも呼びましょうか。
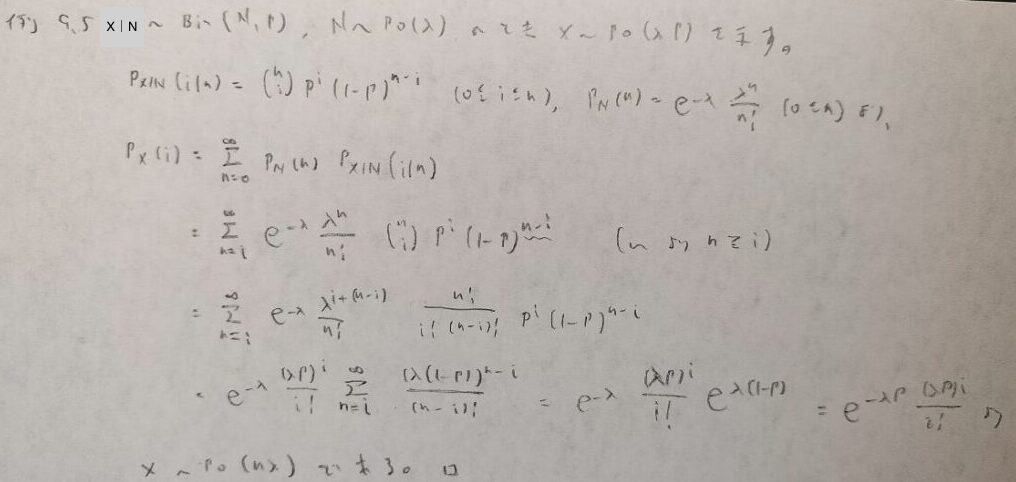
この問題はポアソン・二項分布ですね。
どちらかというとポアソン・二項モデルの方がしっくりくる気がします！
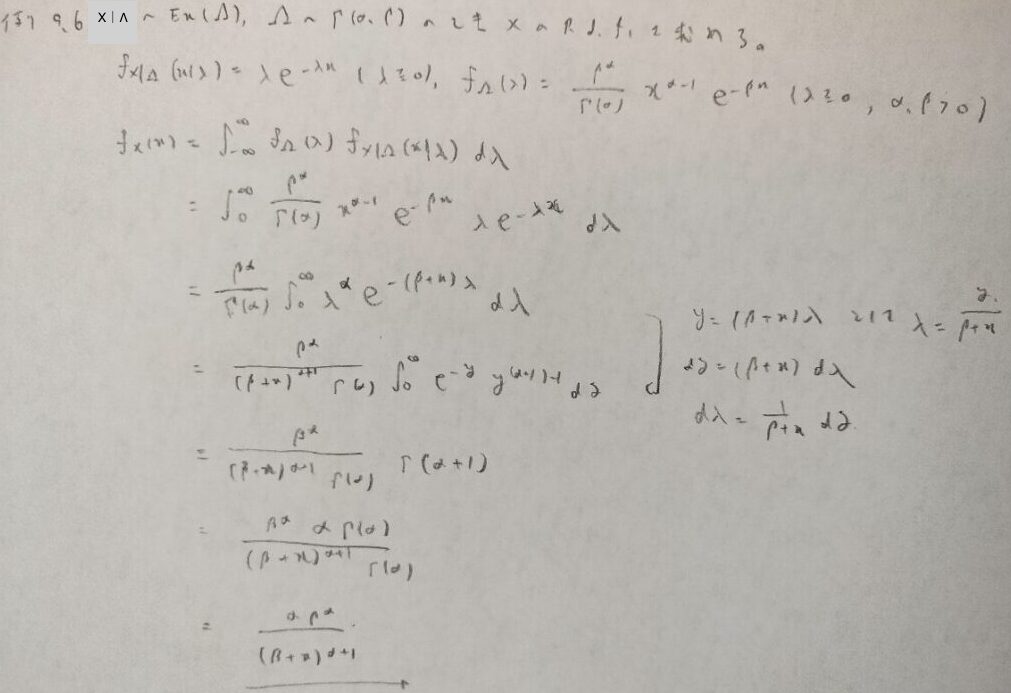
これはガンマ・指数モデルですね！
共役事前分布で有名なガンマ・ポアソン分布です。本来は事後分布はガンマ分布になりますが、今回はガンマ分布のパラメータが整数（アーラン分布）なので負の二項分布に帰着されます。最後のX＋αの分布という部分がややこしいですね。
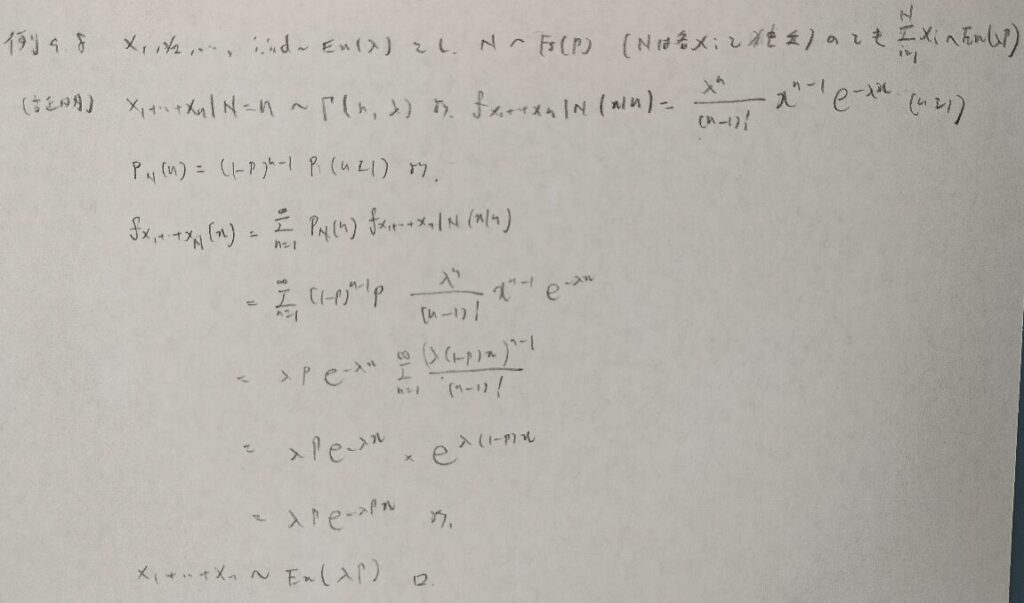
ファーストサクセス・アーラン分布なのか、負の二項分布・ガンマモデルなのか、名付けが大変そうな問題ですね笑
次の問題から条件付き期待値になります。
条件付き期待値は『基本確率 (経済の情報と数理 2)』のラスボス的なテーマです。
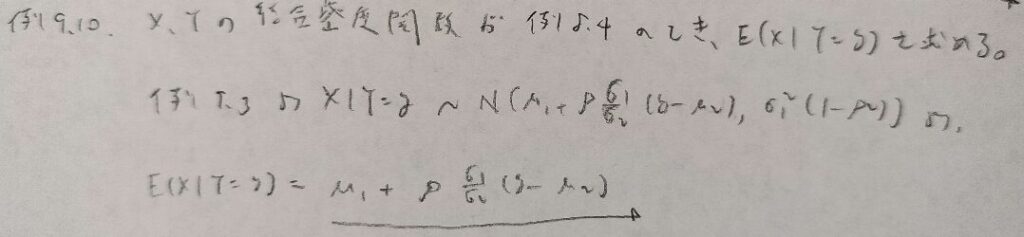
この問題はCrapsゲームと呼ばれています。
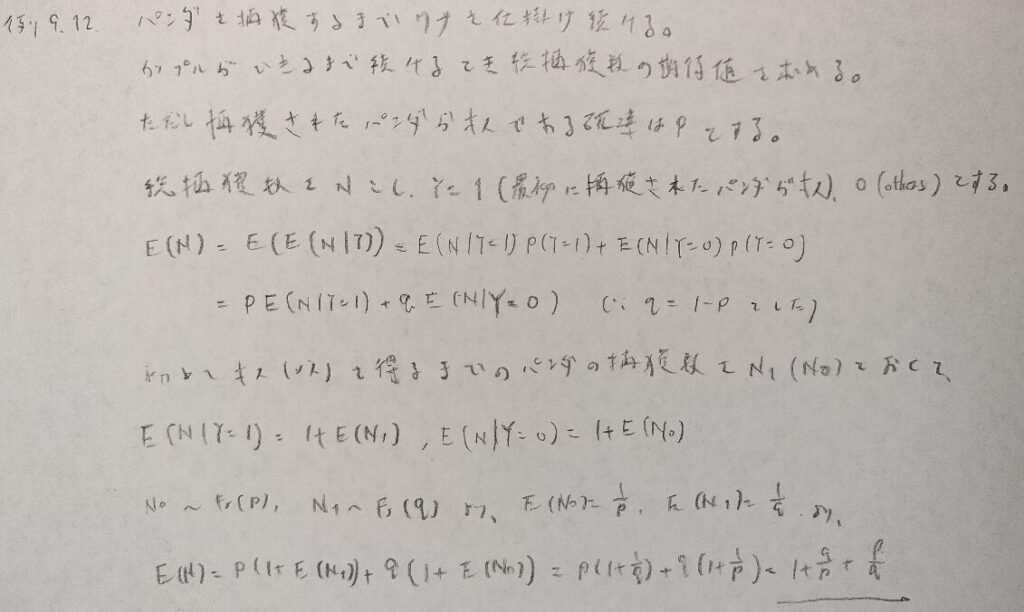
本問のように条件付き確率の有名な公式（EEタイプ）を用いることができるのは、例えば本問ではY＝０やY＝１などで記述できるタイプです。以後の問題の大半は記述ができないので、注意が必要です。混乱を避けるためには頭の中で「EEタイプの公式を用いているんだな」と考えながら立式をしてください。
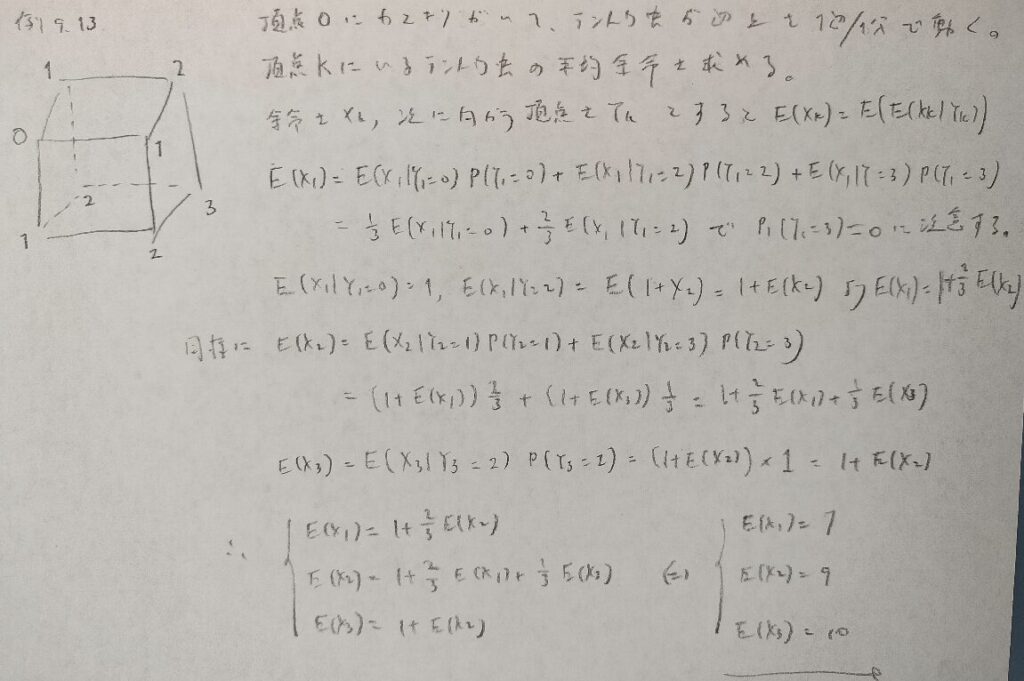
本問題はそっくり同じ問題がアクチュアリー数学に大問として出題されています。類題が出ていないので今後出てくる可能性大です。
条件付き期待値は基本的には難問です。受験数学で勉強した漸化式を用いている感じです。場合分け（条件付け）は１回目や２回目の事象で行うのが定石です。
なるほど！場合分けのコツが分かった気がします！これって言われないと分からない盲点ですよね！
ジョブ・サーチング問題と呼ばれる問題で、アクチュアリー数学に大問として出題されています。これも１度きりの出題です。
クイックソートでも結構回数がかかるなと思いませんか？
『基本確率 (経済の情報と数理 2)』出版時は90年代でしたのでパソコンの黎明期なので、時期的にぴったりの良問ですね。
試行回数がとても大きくなっても回答数が全然増えないことに驚きを隠せません！
基本確率第９章の演習問題
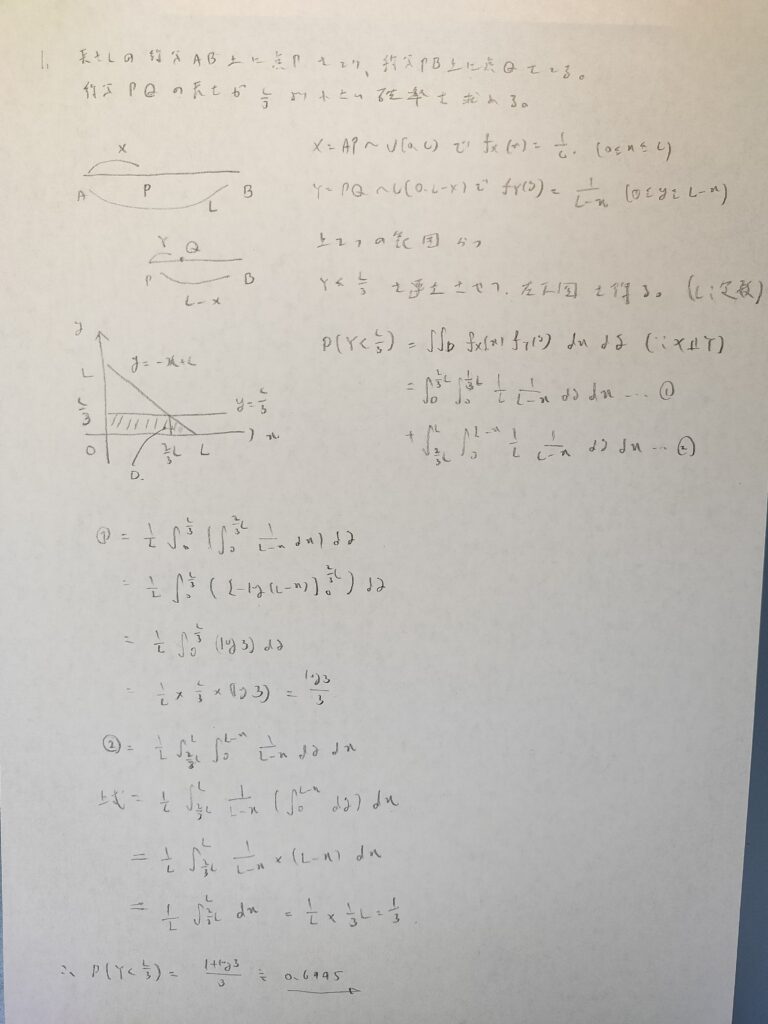
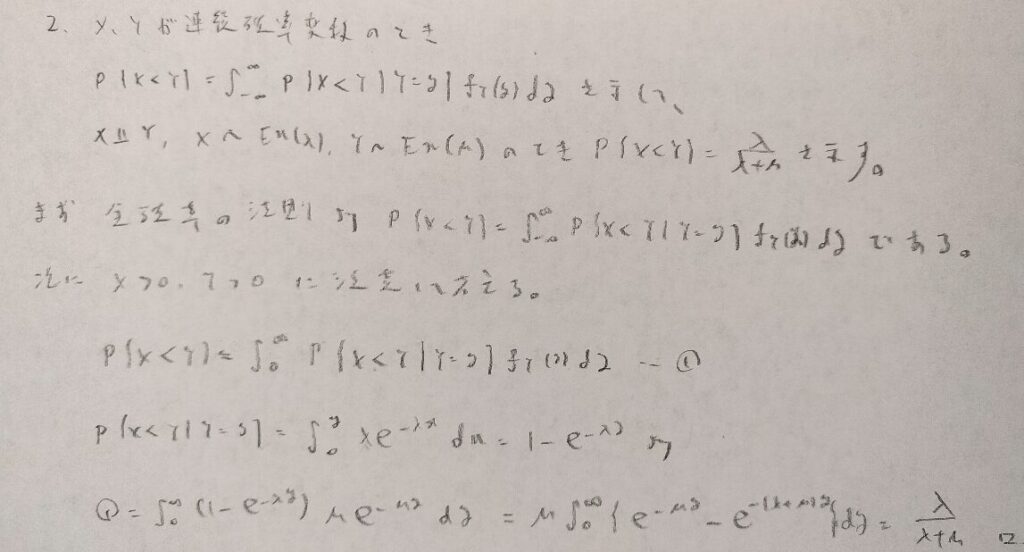
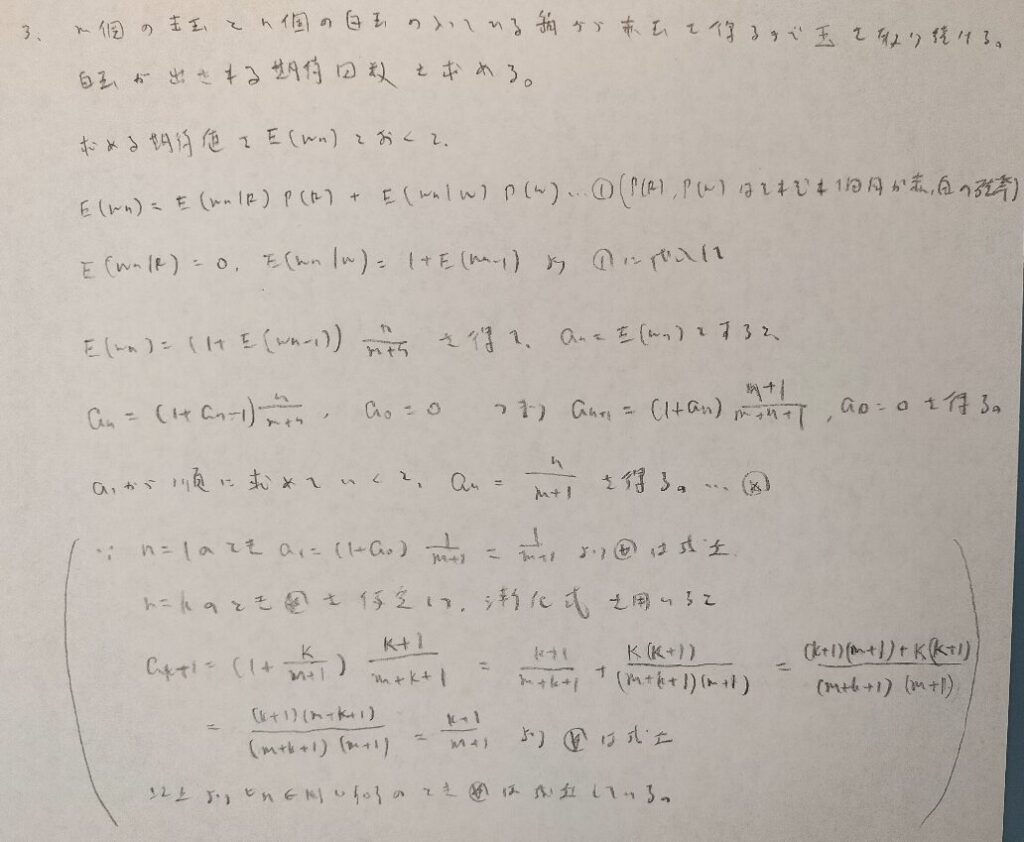
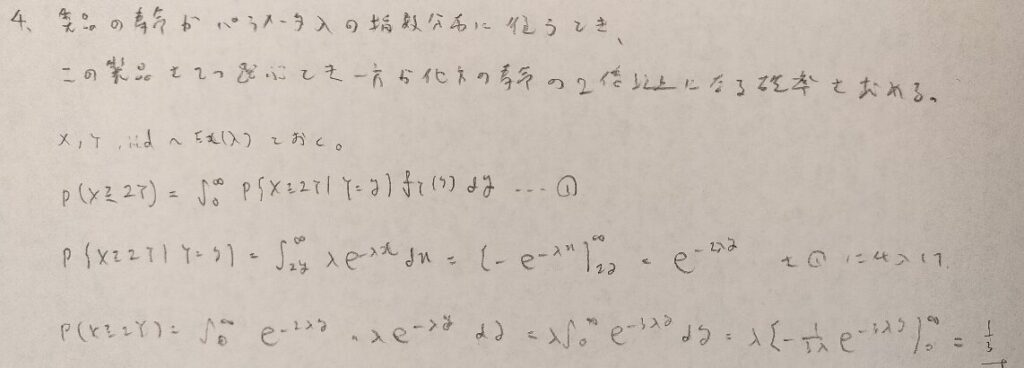
公式解答では2/3となっていますが誤植だと思われます。
基本確率の第１０章の例
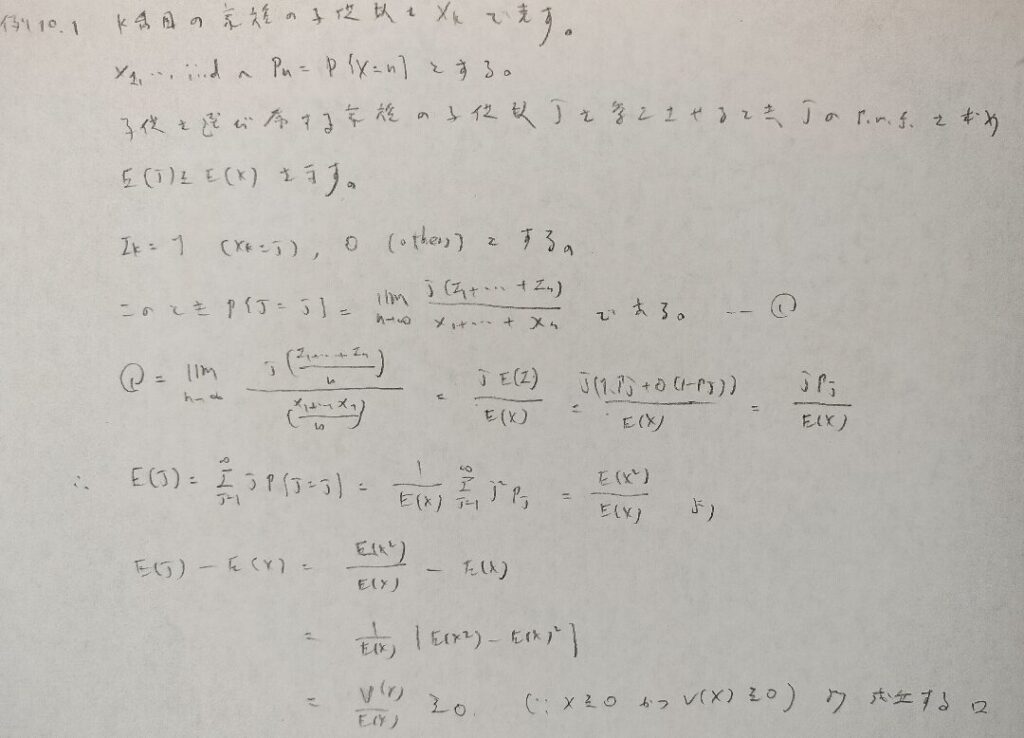
実はこの結果は不思議な結果でして、具体例が次の問題になります。
娘の代で出生率が減った？！と思うような問題です。とても不思議な結果です。
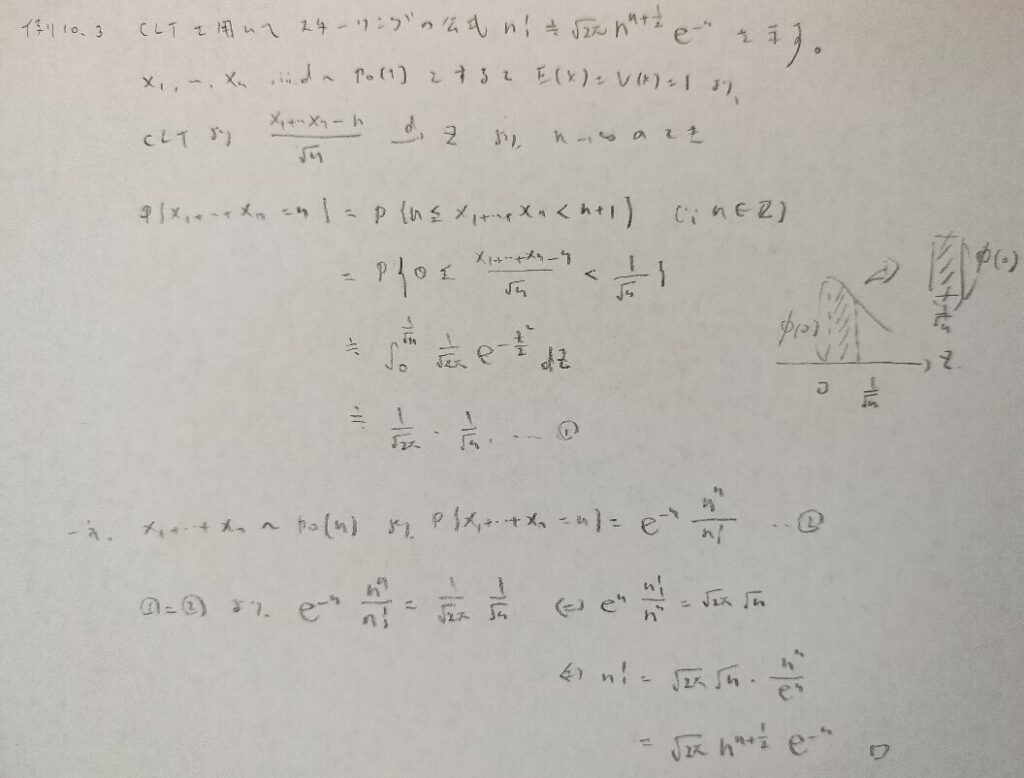
なんとスターリングの公式とポアソン分布が結びつきました。エレガントな証明ですよね。この証明は日本語で書かれた本では『基本確率 (経済の情報と数理 2)』以外に証明は載っていないと思われます。
基本確率第１０章の演習問題
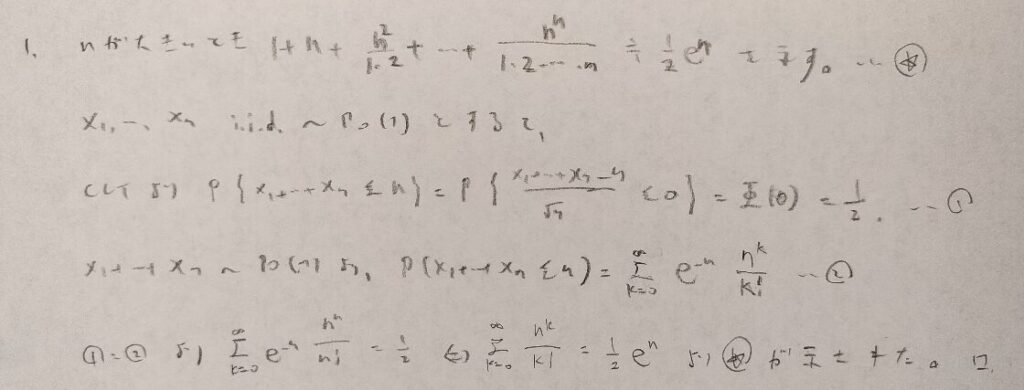
先ほどのスターリングの公式の問題と同様な手順です。CLTを用いた結果と確率分布から求めた結果が一致することから求めたい式を導く流れです。
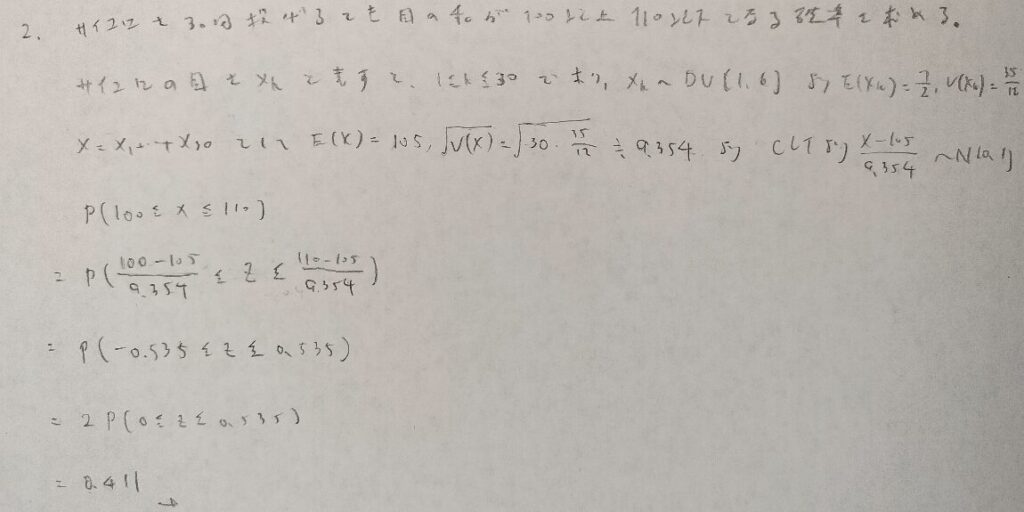
最後の最後の問題は統計検定２級レベルの問題ですが、CLTはとても便利な定理だと実感できたと思います。
以上で『基本確率 (経済の情報と数理 2)』を用いた学習は終了です。特に第１０章は定理の証明がたくさんありますので、数理統計学を勉強する方に本書はとてもおすすめです！
第１部から第４部までお読みくださり、ありがとうございました！
』の各章の解説の最終部になります。 この記事は第４部になります。第１部かのリンクをまとめておきますので、是非とも辿ってくださいね！){kind=link}