アクチュアリー数学や統計検定1級でも2024年度に出題されている順序統計量について解説します。アクチュアリー数学ではベータ分布が利用できるタイプとできないタイプの2つに分けて解説していきます。前者の方はボーナス問題になります。また応用として範囲の分布にも言及します。
順序統計量に関するほとんどの過去問が『確率統計演習 2 統計』から出題されています。まずはこの本の問題に目を通すことをおすすめします。なぜなら本書はアクチュアリー数学の指定教材として指定されている名著であるからです。
本記事からアクチュアリー数学中盤の統計分野になります。前半部の確率分野が未学習の方は以下のページから学習に取り掛かってください!
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
ベータ分布が使える場合(範囲の分布も含む)
平成3年度問1(1)範囲の分布

本問はベータ分布の積率の公式などを覚えていないと時間切れになる問題ですが、アクチュアリー数学の試験傾向をよく捉えている良問です。
平成5年度問3:変化球

かなりの良問です。ベータ分布が絡む順序統計量の差についての公式を知らないと時間内に解けません。類題は2024年11月現在、出題されていません。
平成6年度問1(4)分布関数

平成6年度問1(5)最短の信頼区間
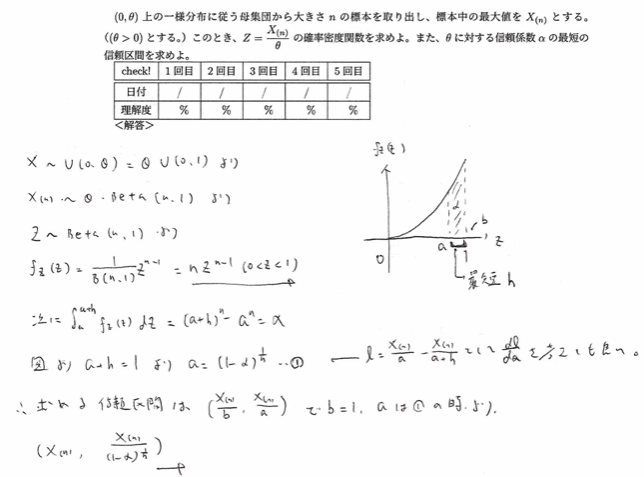
難問です。最後のあたりが難しいと感じます。ポイントは確率密度関数の形より1に近い方が信頼区間は最短になる事実を用いています。
最後の信頼区間の答えのところがわからないので、追加の解説をお願いします。
まず信頼係数がαより、P(a≦X(n)/θ≦b)=αなので、この()の中をθについて解いた式に、上の解答にあるa,bを代入すれば答えです。
今回のようなX(n)/θのような関数をθに関するピボットと言います。この名称はアクチュアリー数学では範囲外です。
平成12年度問2(7)分布関数の順序統計量

別解の方が絶対に楽です。ベータ分布の知識が使えるためです。
平成13年度問2(3)順序統計量の差の分布

基本的な問題ですが、ベータ分布の高次モーメントの公式は既知とします。
平成22年度問1(9)中央値

推定量の分散を2つ考えます。推定量は何か?の部分で混乱しないように注意が必要です。
2019年度問1(6)絶対値

これが小問?!となるような計算量の多さに驚愕ですよね。アクチュアリー数学は2018年度から明らかに難化しています。
ベータ分布が使えない場合
昭和62年度数学Ⅰ問4:積率母関数の利用

今後は誘導形式で出題されることが予想されます。
平成元年度数学Ⅰ問1(9)指数分布

指数分布の最小統計量は公式として覚えましょう。壊れる時間が増していくと考えれば納得できる結果です。
平成6年度問4:指数分布の意味

この問題は岩沢先生の『リスクを知るための確率・統計入門』を読んでおくと単純な問題に思えるはずです。
感覚的な考え方としてはn個の機械があってその最小統計量とは、どれかの機械が壊れる時間なので1個の機械が壊れる時間が(1個と比べてn個あるので)期待値は1/nつまり(どれかの機械という意味で)n倍壊れやすい(すぐの時間で壊れてしまいやすい)ので、Γ(1,n)が最小統計量の従う分布になります。そして残りn-1個の機械において、最初に壊れる機械(つまりX(2)-X(1))が従う確率分布はΓ(1,n-1)になります。
平成9年度問1(7)図形的考察
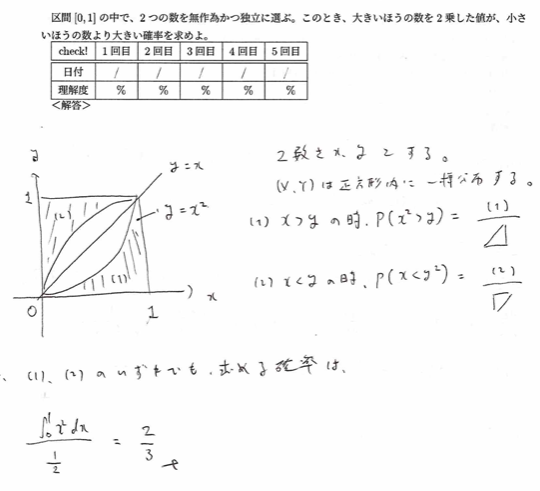
図形的な考察を必要とする問題は確率変数を素直に設定してみることが大事です。
平成14年度問1(5)幾何分布

幾何分布とファーストサクセス分布と指数分布の最小統計量の公式は覚えておきましょう。
幾何分布の場合について解説します。本問のような2つの場合を考えます。一般の場合も同様に考えられます。幾何分布の定義は初めて成功するまでの失敗回数なので、2つの確率変数を考えるときの最小統計量は、少なくとも1回成功するまでに失敗した回数なので、1-q^2の確率が1回成功する確率と考えて幾何分布の定義に従うと結果が得られます。
平成23年度問1(2)円の問題

平成25年度問1(5)変化球

難問です。ヒントがないと解くのは厳しい難易度です。
どうしても分からない場合は、nを小さい順から考えて推定するしか方法はないでしょうね。
難易度を高くしているのは2番目の関係式の存在です。大学入試ではお目にかかることがないので、多くの方にとって初見問題となります。
2018年度問3:順序統計量最難関


(1)は基本問題ですが、(2)以降が難問です。ただ(2)の最後の括弧はμであると計算せずにわかります(不偏推定量となると書かれているので)。(3)はスターリングの公式を駆使していくだけですが、とても時間がかかります。
スターリングの公式は覚えてしまいましょう!式変形をすると円周率の近似式にもなっています。
範囲の分布(ベータ分布が使えない場合)
平成25年度問3(2)標本範囲の分布


答案の図よりも、普通にx(1),x(n)の範囲が0以上1以下という条件から、sとrの領域を図示していくのがオーソドックスだと感じます。
順序統計量に関するほとんどの過去問が『確率統計演習 2 統計』から出題されています。まずはこの本の問題に目を通すことをおすすめします。なぜなら本書はアクチュアリー数学の指定教材として指定されている名著であるからです。
公式証明系(標本範囲の分布など以外)
昭和62年度問5:一般公式

アクチュアリー数学では結果のみ覚えておけばOKです。
平成8年度問3:ベータ分布

定義に基づいた厳密な証明になります。簡易的な公式証明は下記で体系的に解説しました。
(2)の途中でCが出てくる理由は、n個中でi個がx以下の値をとる確率変数ということからです。確率変数Xは標準一様分布に従うことにも注意しましょう。
平成16年度問4:分布関数

2022年度問5:相関係数


(1)の中盤までしか簡単ではありません。以後は難問です。しかし相関係数などが2023年度の試験に出なかったことを考えると、今後狙われる可能性が高いです。解答途中で出てきた共分散を求めるときに用いた確率変数の差の分散を考える式が本問のテクニック部分です。これを思いつけないと本問は合格ギリギリの点数となります。
順序統計量に関するほとんどの過去問が『確率統計演習 2 統計』から出題されています。まずはこの本の問題に目を通すことをおすすめします。なぜなら本書はアクチュアリー数学の指定教材として指定されている名著であるからです。