難関資格のアクチュアリー数学の中で難易度が低い分野が中心極限定理の分野です。覚えておく公式はCLTの１つだけで、あとはこの定理を個々の問題に適用していく流れになります。中心極限定理は平成12年度から出題されており比較的新しい（古くはない）分野となります。
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
標準正規分布表の考えを用いる問題
平成12年度問１（７）左半分
困ったら実際に中心極限定理を適用してみましょう。そして問題文と照らし合わせていると解法が浮かび上がります。最初の問題にしては慣れていないと苦戦する難易度かも知れません。
平成20年度問１（４）連続化
とても良い問題です。最後は標準正規分布表の考えを用います。
2019年度問１（４）積分の形
誤差の問題
平成14年度問１（７）平均の誤差
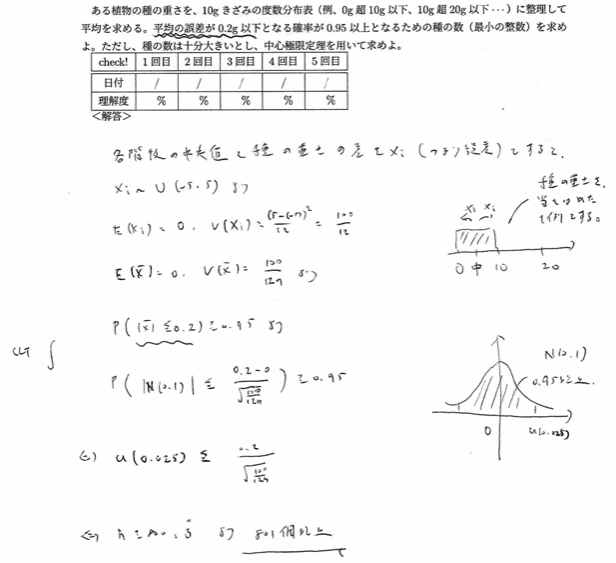
階級値に注目して新たな誤差を表す確率変数を設定します。ここを思いつくのが難しいです。
平成15年度問２（７）四捨五入
新たな一様分布に従う確率変数を設定することが本質的です。
平成16年度問１（６）五捨六入
図に表現してみることが大事です。
チェビシェフの不等式との関連
平成25年度問１（４）チェビシェフの不等式
kの値を吟味することが本問の醍醐味です。
2021年度問１（５）四捨五入との融合
応用問題
平成4年度問４：中心極限定理の応用
平成17年度問１（６）カブトムシ問題
ｋが従う二項分布を設定できれば勝ちです。
2022年度問１（４）カブトムシの再来
前回よりも難易度が格段に上昇しています。特に後半の問題が難問です。
平成18年度問１（３）サイコロの差
AとBの点数の差と言われたら絶対値をつけます。
平成23年度問１（４）変化球
前半の問題は中心極限定理を用いない変化球タイプの問題です。
平成27年度問１（３）勝ち数
勝ち数をnと置くと後は自然と解けます。
平成29年度問１（４）複合分布
試行回数をNとする確率変数を考える必要がります。そのため複合分布になります。複合分布の期待値と分散の公式も覚えておきたいところです。
2020年度問１（４）七捨八入
二項分布の問題であることに注意しましょう。また、僕は本問を解いた時に作問ミスか？とメモしましたが、そんなことはなかったです。なぜなら後半の問題は前半で求めた確率変数をそのまま用いるためです。
2023年度問１（５）計算量の増加
とにかく最近のアクチュアリー数学は計算量が増加している傾向にありますね。
その通りです。しっかりと公式を覚えて過去問を解いて取れる問題はしっかりと取ることを意識して本番に臨みたいですね。
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
