本記事ではアクチュアリー数学の中で変数変換と合成系の過去問題を扱います。他の章と比べると覚えるべき公式は少ないですが、岩沢先生の『リスクを知るための確率・統計入門』には変数変換のあまり知られていないテクニックが掲載されておりおすすめです。
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
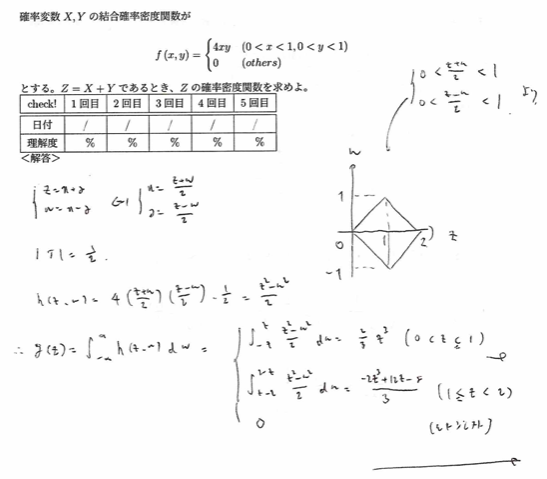
和の分布
昭和62年度数学Ⅰ問2:変化球

ガウス積分の公式は覚えましょう。
平成2年度数学Ⅰ問3:コンデンサー

お気づきだと思いますが、答案のパラメータの分子と分母が逆です。すみません。
平成6年度数学Ⅰ問2:対数正規分布

後半の問題が技巧的ですが素晴らしい問題です。
平成10年度数学Ⅰ問3:ガンマ分布の分布関数

平成15年度問1(3)ガンマ分布に帰着

最初の式をガンマ分布と気付けるか?が勝負です。
平成15年度問1(5)負の二項分布に帰着

平成18年度問1(2)キュムラント

平成19年度問1(3)ファーストサクセス分布

ファーストサクセス分布の積率母関数を覚えておきましょう。
平成21年度問1(2)正方形
差の分布
昭和63年度数学Ⅰ問3:シグマの範囲に注意

難問です。対称性などを用いて計算量を減らしましょう。
積の分布
平成6年度数学Ⅰ問1(3)ポアソン分布

最後にひっかけがあります。見逃さないようにご注意ください。
平成11年度数学Ⅰ問3:積分範囲に注意

商の分布
平成3年度数学Ⅰ問1(2)コーシー分布

平成17年度問1(4)ラプラス分布と第2種パレート分布

平方変換
平成2年度数学Ⅰ問1(7)F分布との融合

アクチュアリー数学においてt分布やF分布の確率密度関数を覚えていないと時間切れになります。
平成27年度問1(4)ガンマ分布の商

F分布に帰着できない計算が要求されるタイプです。
式変形においてガンマ分布の性質をふんだんに使っています『弱点克服 大学生の確率・統計』に計算テクニックがたくさん掲載されておりおすすめです!
2020年度問1(3)分布関数経由

特殊なタイプで難問です。この方法に気付けないと2回変数変換を行うことになりタイムロスになります。
平方和の分布
平成5年度数学Ⅰ問1(4)カイ2乗分布

平成13年度問1(8)半径の分布

統計検定1級にも類題が出題されている良問です。最後の方は慣れていないと難問になります。
合成系
平成元年度数学Ⅰ問1(10)複合分布との融合

平成2年度数学Ⅰ問2:待ち時間の分布

「待ち時間の分布を求めよ」とは分布関数を求めよという意味のようです。t=xという瞬間に待つ確率よりも、t=x以内で待つ確率という意味合いが強いためだと思われます。t=0のときN=0として値が0でなく1/3となる理由は同時に3人来るという感覚だと考えます。
平成5年度数学Ⅰ問1(3)通話料金

期待値と分散があるので、積率母関数を用いて一気に求めた方が良いですね。
平成7年度数学Ⅰ問4:書類決済

複合分布の期待値の公式が使えるときは使ってしまいましょう。具体的には期待値のみ欲しい場合に効果的です。
以上のように変数変換や合成系の過去問は、序盤の頃の過去問が難易度が高く、中期では典型問題に偏り、近年に難易度が再び上昇しています。何度も学習して身につけて得点源にしたい分野ですね。
本記事ではアクチュアリー数学の中で変数変換と合成系の過去問題を扱います。他の章と比べると覚えるべき公式は少ないですが、岩沢先生の『リスクを知るための確率・統計入門』には変数変換のあまり知られていないテクニックが掲載されており、おすすめです。
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。










