本記事はアクチュアリー数学で頻出の一様分布を扱います。図形問題との絡みも含めれば最も基本的で正規分布についで応用が効く分布です。
『アクチュアリー試験 合格へのストラテジー 数学 第2版』は合格に必須の公式が掲載されている唯一の参考書です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
また本記事の分野では一様分布特有の考え方を用いる問題を学ぶことになります。本章の問題ネタは『明解演習 数理統計』です。こちらもお手元に置きながらの学習をお勧めします。
本記事では膨大な問題の中からいくつかのカテゴリーに整理して一様分布と図形問題を整理していきます。
順にご覧くだされば幸いです。
1次元上での一様分布(待ち時間の問題)
昭和62年度数学Ⅰ問1(7)基本問題

これ系の問題の解法を初めて知った時は感動しました。一様分布は地味ながらも普段の生活に応用できる実用的な確率分布だったのです。
平成11年度数学Ⅰ問1(7)鉢合わせ

1次元上の一様分布(待ち時間の問題以外)
平成4年度数学Ⅰ問1(3)正弦関数

有名なひっかけ問題です。1対1対応になるために場合分けをして考えます。
2020年度問1(2)離散と連続の期待値

確率変数YをXで表すところが難しいですね。このタイプの問題は頻度は低いですが良問です。
2次元上の一様分布(三角分布関連)
平成6年度数学Ⅰ問1(2)三角分布に似た分布

平成12年度問1(5)三角分布

確率和(面積)1であることなどを考えると自然と結果が得られます。具体的にはYにーがついた場合はU(-1,0)と考えられるので、和の分布と考えることができることを利用します。記述の場合は実際は差の分布として場合分けして求めますが、この問題は先ほどの問題と異なり、三角分布になります。
平成12年度問3:台形分布
台形分布という言葉は文献にはなく、三角分布の亜種として勝手に命名させていただきました。

Yの分布の定義を20分を超える部分としているのは、Y~U(0,20)つまり左端を0にしたいためです。
Zの分布は対称的な図形になることと、確率和1に注意して図示します。台形の形が変わる部分は20と30のうち小さい数字の方が優先されます。
確率の考えだけで平均所要時間などまで判明するのってすごいことだなって思いました!
平成18年度問1(4)3つの和

難問です。どれか2つを選んで三角分布を作って、もう1つの確率変数とを合わせた和の分布を考えます。
2023年度問1(3)平行四辺形

きちんと計算したほうが推測で答えるよりも良いです。(体験談)
2次元上での一様分布(三角分布関連以外)
昭和62年度数学Ⅰ問3:ベータ関数の利用

積分計算を回避するためにベータ関数の知識を駆使します。
平成元年度数学Ⅰ問2:正方形

原点を中心とする図形の対称性に気が付けば共分散が0であることは一瞬でわかります。しかしyの確率密度関数を求める場面など、ひっかけ部分が多い印象です。
平成元年度数学Ⅰ問1(8)鋭角三角形
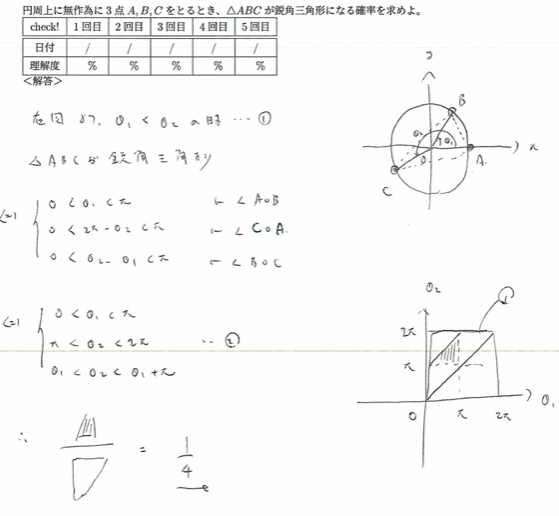
アクチュアリー数学では準公式のような問題です。直角三角形となる確率は0なので鈍角三角形となる確率は0.75になります。
ポイントはAを定点とし、BとCの角に大小関係を設けることです。それにより図示による考察が可能になります。
平成5年度数学Ⅰ問4:三角形ができる確率
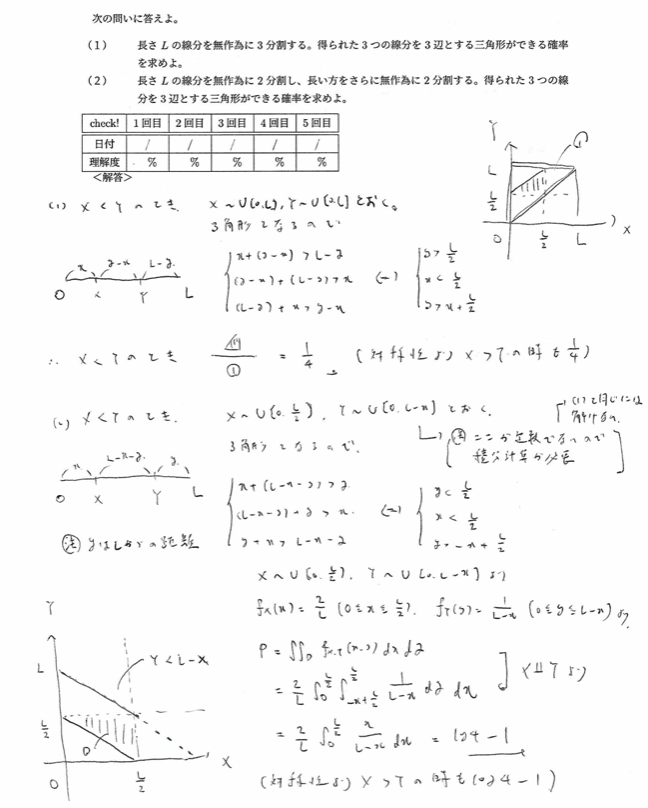
XとYの大小関係を設定する必要があります。定数か変数かによって図形的な処理が異なるのでご注意ください。要するに積分計算が必要か否かの違いです。
平成6年度数学Ⅰ問4:半円
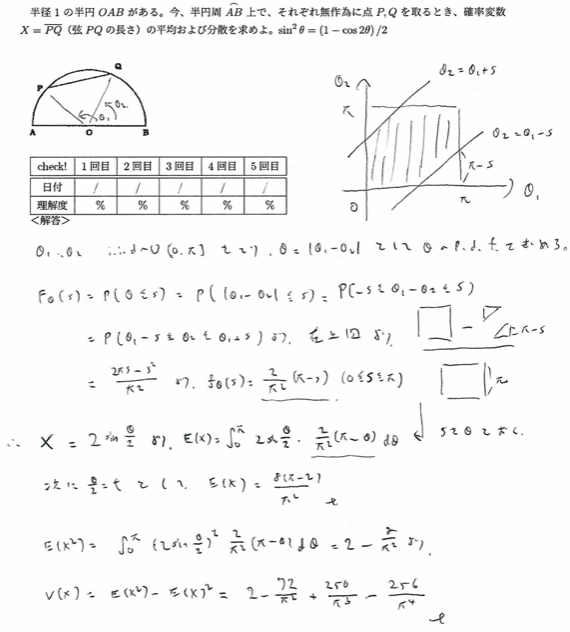
PとQが任意ですので角度の置き方に注意しましょう。分布関数から考えていくことがコツです。
平成7年度数学Ⅰ問1(2)最大最小

場合分けに気付ければ典型問題になります。
平成7年度数学Ⅰ問1(5)対称性

Xの期待値も同時分布から一気に計算しています。色々と実力差が出てくる良問です。類題が数学検定1級で出題されています。
平成8年度問1(2)回転する長方形
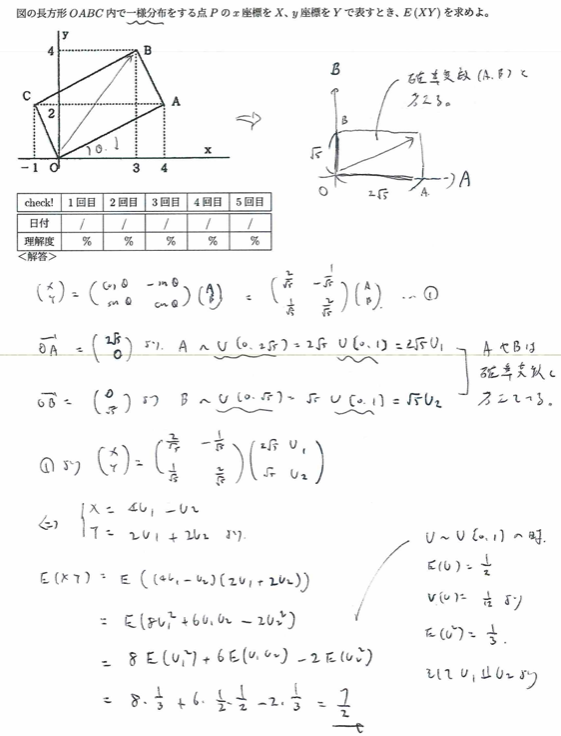
本問はとても良い問題です。2変数の確率変数の変換の問題です。回転行列を持ち出して、標準一様分布との関係性も用いて効率よく計算したい問題です。
平成15年度問1(7)三角形の面積
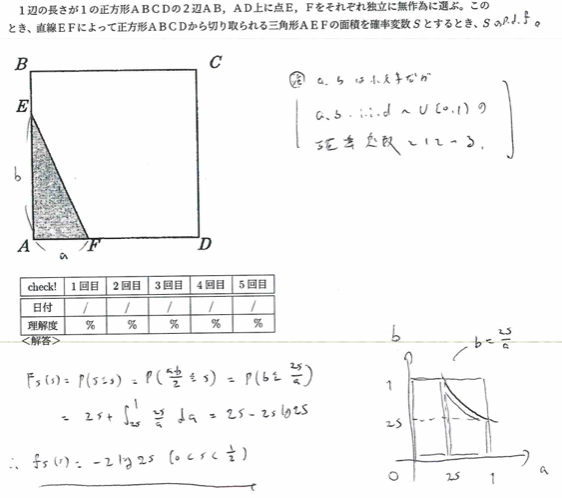
小文字のsは実現値であることにご注意ください。大文字のSをa,bで表して考えていきます。
確率密度関数が直接わからないときは、分布関数を経由して求めるのが定石です。
平成16年度問1(6)半円内の直角三角形
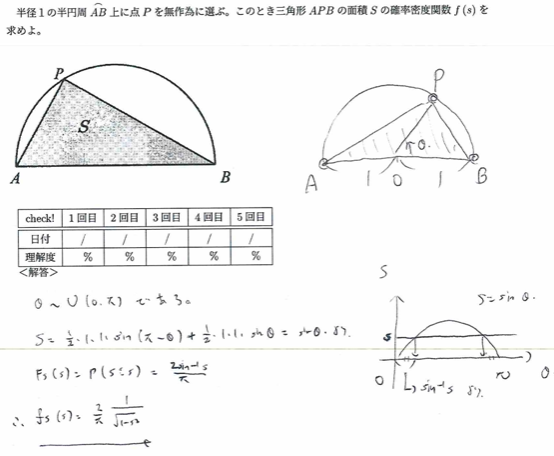
難問です。θの置き方と、分布関数の出し方を見抜けるか?の勝負です。
平成17年度問1(10)半円内の三角形
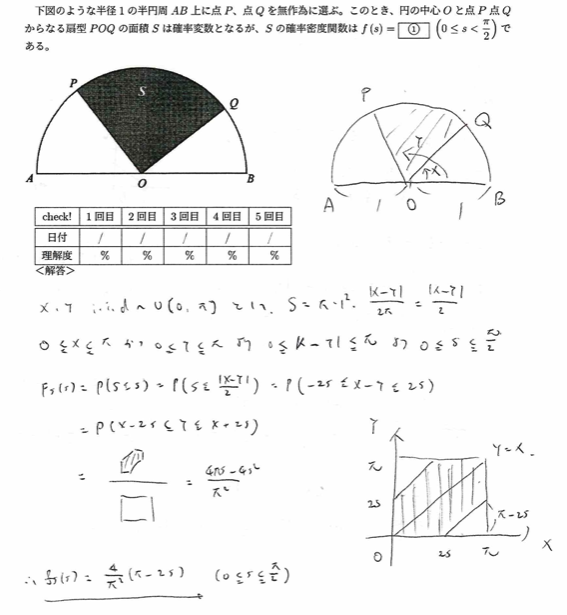
解答中の第3行目の不等式の3つ目の不等式でSの方にXやYを代入します。訂正すみません。
平成18年度問1(5)三角形の面積の期待値
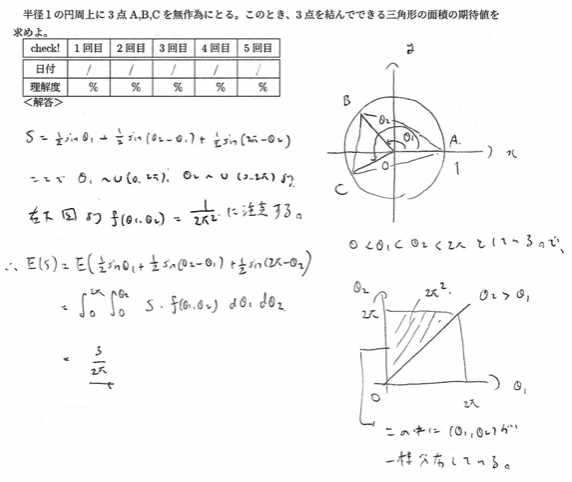
同時分布を出す際に混乱しなようご注意ください。
平成19年度問1(5)六角形
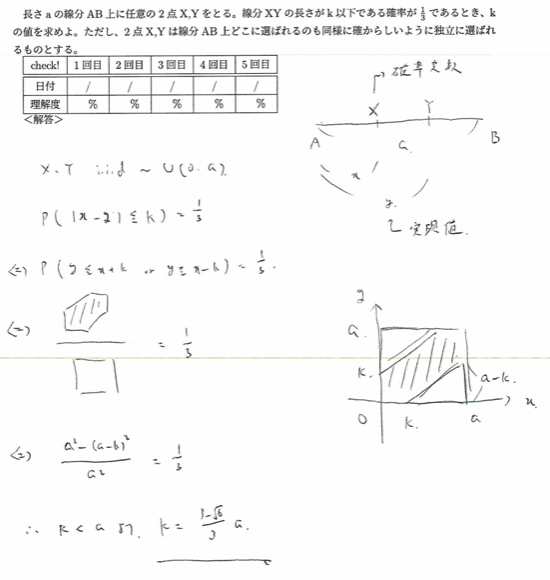
基本的な問題なのでしっかりと得点しておきたいですね。
平成20年度問1(5)正方形

最後の図示では場合分けが必要です。考察忘れがないように注意しましょう。
この問題はxと置くところもやや難しいんですよね。慣れたいものです。
2022年度問4:ルーレット
本記事での最難関問題です。2022年はアクチュアリー数学の問題難易度が最難関の年です。
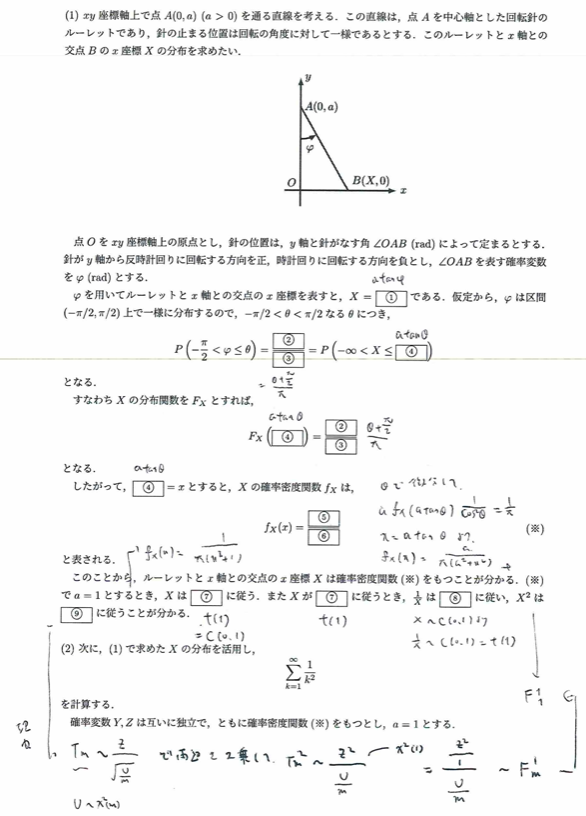

2022年度から問題量が一気に増加しました。一昔前のアクチュアリー数学と比べると解答に必要な量が1.5倍近くになっているそうです。
3次元上での一様分布(ディリクレ分布の利用)
平成16年度問1(4)ディリクレ分布の利用

これぞアクチュアリー数学という問題です。初見で気づける方はかなりレアです。
3次元上での一様分布(ディリクレ分布の利用以外)
平成3年度数学Ⅰ問1(10)四捨五入

[-0.5,0.5]の一様分布に従う問題なので平行移動により[0,1]に直してから考えるのがコツです。初見ではかなりの難問ですが、現在では頻出問題となっています。
平成5年度数学Ⅰ問1(2)二次方程式が実数解を持つ確率
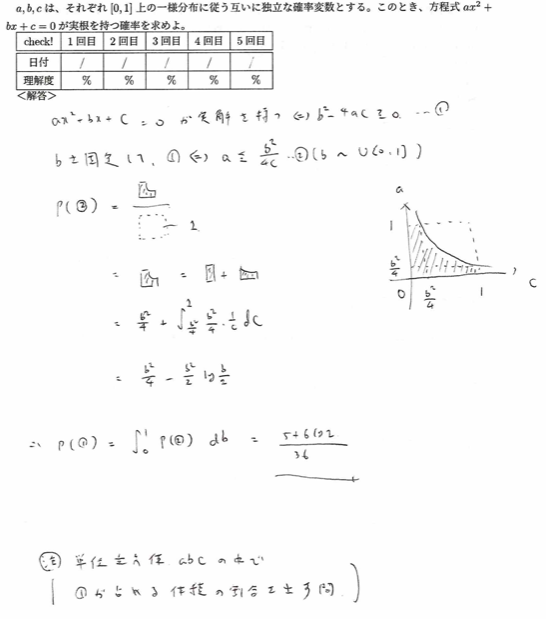
次数が多いbを固定するのがコツです。数学検定1級にも類題が出題されています。ただし数検の場合は2次検定で、アクチュアリー数学では小問としての出題です。アク数の難易度の高さが垣間見える一例です。
『アクチュアリー試験 合格へのストラテジー 数学 第2版』は合格に必須の公式が掲載されている唯一の参考書です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
また本記事の分野では一様分布特有の考え方を用いる問題を学ぶことになります。本章の問題ネタは『明解演習 数理統計』です。こちらもお手元に置きながらの学習をお勧めします。





