本記事では漸化式の問題を解説します。アクチュアリー数学の中では比較的パターン化されている分野となります。ただし破産の確率などの知識問題も出題されます。本記事にて効率の良い学習をしていきましょう。
『アクチュアリー試験 合格へのストラテジー 数学 第2版』は合格に必須の公式が掲載されている唯一の参考書です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
リセット型
このタイプは方程式の問題に帰着されますが、難しい場合は無限級数の問題として処理しましょう。方程式の立式はリセットの考え方が基本です。
実はここ最近『基本確率 (経済の情報と数理 2)』からの出題が目立ちます。平成中盤は本書から同じ問題が大問2の確率の問題で出題されている傾向がありました。近年でもアレンジはされていますが本書をネタとした問題が多々見受けられます。
昭和62年度数学Ⅰ問1(4)コイン

平成3年度数学Ⅰ問1(5)巴戦

初戦でAが勝つか負けるかで2通りの場合分けがあります。この問題では後半のパターンのリセットのタイミングが難しいです。
平成6年度問1(1)リセットの区切り

平成18年度問2:サッカー

繰り返しがあることに気づけるか?の問題です。今後小問集合で出題される可能性があります。結局最後は確率0.5で公平なゲームだと判明します。
平成21年度問1(1)2元型

記号の設定法を覚えてしまいましょう。
2項間漸化式
平成8年度数学Ⅰ問1(1)メニュー問題

あまり見ないタイプの漸化式です。
平成15年度問3:2次元ランダムウォーク

n秒後の原点からの蟻の位置の期待値は、半径ルートnの同心円上以下という興味深い結論になりました。
問題文の独立というヒントは、Xn-1のときまでの情報がなんであれ、次のXnへどう移るかには無関係であるからですね。すると当然ZnにもXn-1のときまでの情報は関係がないことになります。
3項間漸化式(破産の確率)
平成7年度問3:等確率の意味

公式を覚えましょう!2023年度の近年の問題でも出題されています。ただし近年は「これは破産の確率だ」とわからないように問題が作られています。
漸化式の立式は初めにAが勝って破産する場合と、初回でAが負けて破産する場合の3項間漸化式となります。初期条件は所持金が0円の時は確率1で破産し、所持金が全額の場合は確率0で破産します。両者の確率が等しい場合は、所持金が多い方が破産しにくいという直感的な結果となっています。例えばAが2円でBが3円持っていたとき、Aが破産する確率は0.6となります。これはAの方がBより少ない所持金であるためです。
平成22年度問1(1)ランダムウォーク

破産の確率の応用では簡単な方です。
2023年度問4:ポーカー
このポーカー問題は本記事の中で最も難しい問題です。破産の確率が終盤に控えているので漸化式に分類しましたが、今後ポーカーの各役の生ずる確率を求めさせる問題は小問集合で考えられるので、本問開始前にまとめておきます。
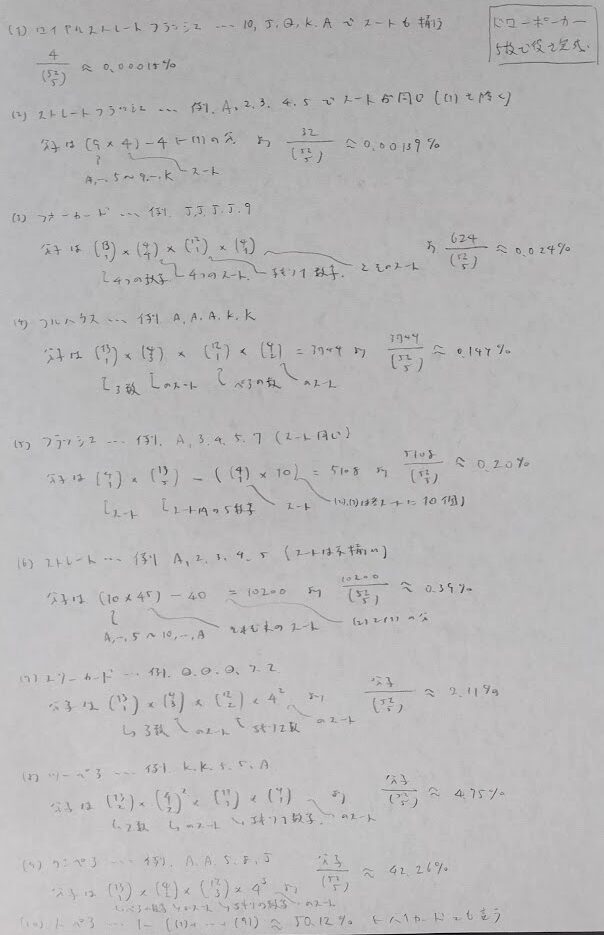

⑨の公式の模範解答がわからなかったので、素直に期待値計算を工夫して考えました。下記にこの方法の根拠も含めて紹介します。
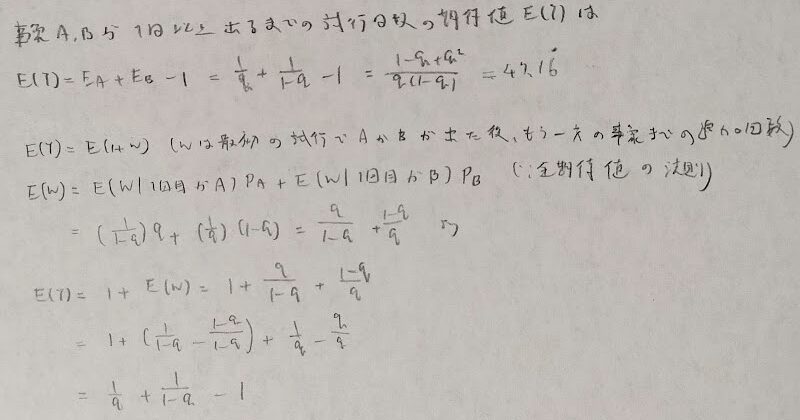
次の連の問題は、素直に問題文に従って◯と|で考えましょう。関連する連検定は次の記事に掲載しています。

とにかく処理量が多い問題です。序盤から難しいですね。そして最後のは破産の確率です。
僕は2023年度の受験時に「序盤の問題と破産の確率の部分以外は捨てよう」と諦めてしまいましたが、実際はもっと点が取れたであろう大問構成でした。
アクチュアリー数学ではこのようなことが頻繁に起きます。ザッと問題文全体に目を通しておくことが大事です。
3項間漸化式(破産の確率以外)
平成4年度数学Ⅰ問4:表が続けて2回出ない

4項間以上の漸化式
平成21年度問2:負の二項分布の一般化

解答の図が書けること、そして最後の期待値についての洞察が必要な良問です。
平成26年度問2:尻尾確率


最後の計算がとても難しいです。本番で出たら飛ばした方が良いです。また尻尾確率を用いた期待値や分散の計算は以来未出です。(2025年11月現在)そのため大事な問題となります。
連立漸化式
平成3年度数学Ⅰ問2:立方体

n=0では成立しない連立漸化式です。そのため遡る際はn=1までに注意しましょう。
すなわち対称性が成り立つのがn≧1のときです。
平成24年度問2:0に戻すルール


問題文の誘導に乗れない時は1つの目の画像の解答のように図式化することが大事です。そこから見えてくる情報に助けられることがあります。
平成26年度問1(2)玉取り

素朴な設定ですが嵌ると解けません。確率和1に気づけるか?が勝負です。
2022年問1(1)最初の問題の最難関

問1(1)からこのような問題が出てきたら心折れそうです。とにかく処理量が多い問題で歴代の問1(1)で最難関です。
期待値の漸化式
平成14年度問3:蜘蛛問題
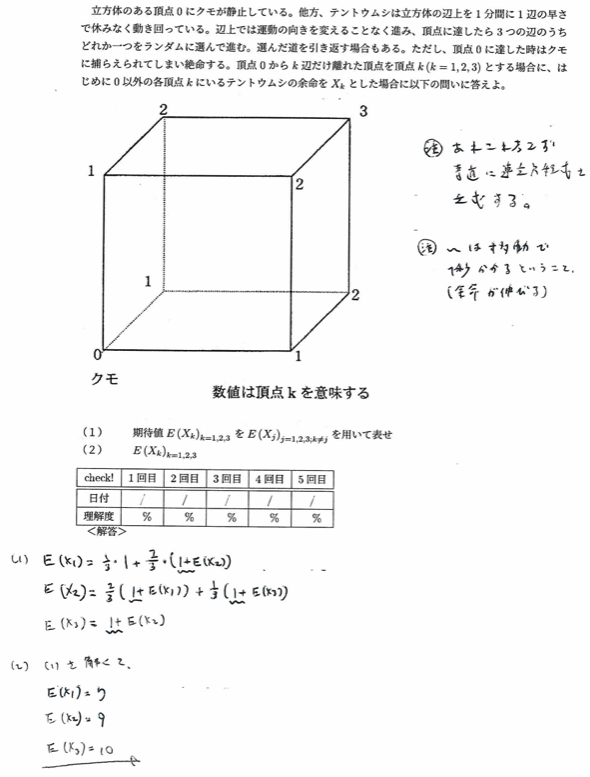
(小問がなければ)初見では絶対に解けない問題ですが、教科書に掲載されても良いような教育的良問ですので第1問(1)で出ても不思議ではないです。
平成17年度問3:飛越禁止

見かけよりも立式は簡単な問題です。ある意味ファーストサクセス分布の応用問題かも知れません。
平成25年度問2:期待値の連立漸化式


期待値の漸化式が前半部から登場しているので難問です。ただし問題設定は素晴らしい良問です。ただし最後の最後の漸化式を解く部分がとても難しいです。本番では捨てないと時間切れになります。
2018年度問2:プレミアム問題



本問は確率漸化式と期待値の漸化式と連立漸化式の融合で途轍もない難易度です。漸化式分野の最難関として良い難問です。
2019年度問2:確率変数の分解


前年度と比べると得点を上げられる問題構成ですが、それでも難問です。ここ最近のアクチュアリー数学の難易度の上昇の仕方は異常です。
実はここ最近『基本確率 (経済の情報と数理 2)』からの出題が目立ちます。平成中盤は本書から同じ問題が大問2の確率の大問で出題されている傾向がありました。近年でもアレンジはされていますが本書をネタとした問題が多々見受けられます。
漸化式は問題が解きやすいと得点源になる分野です。過去問+上記の本を片手に乗り切りましょう!!




