アクチュアリー数学の過去問でベイズ統計、複合分布、条件付期待値などを学習します。ここは学習の習熟度が解答時間に大きく関わってくる箇所です。
『アクチュアリー試験 合格へのストラテジー 数学 第2版』は合格に必須の公式が掲載されている唯一の参考書です。お手元に置いて本記事をご覧くだされば学習効率が上がります。本書に載っている複合分布の公式は要確認です!
章を通して全体的に幾何分布とファーストサクセス分布と指数分布には無記憶性があることを知っていると、無記憶性を用いる問題で計算を大幅に短縮させることができます。
本記事を学習される前に上の3つの記事に目を通された方が学習効率が上がります。
ベイズの定理
平成19年度問1(1)Zで作られている割合

典型問題からひねった出題です。P(Z)が出てくる式を作り出すことがポイントです。2025年11月現在、類題の出題がないためかなり要チェックの問題です。
平成25年度問1(1)変化球

これが第1問で出題されても落ち着いて回答したいですね。
あらかじめ過去問演習をしておくことは大事ですね。
無記憶性あるいは類似問題
平成元年度数学Ⅰ問1(1)ひっかけ問題

平成9年度数学Ⅰ問1(1)幾何分布のパラメータ

平成17年度問1(9)アクセス問題

ポアソン分布と指数分布の意味を捉えられているか、無記憶性を把握できているかの良問です。
条件付き分布
平成3年度数学Ⅰ問3:多重積分

条件付き分布の一般形の式を用います。割と頻出のタイプです。
ただしそれ以外は実験をしないと方針に気が付きにくく難問ながらも典型問題になりそうな予感がします。
平成5年度数学Ⅰ問1(5)範囲に注意

最後の範囲に注意します。小問で穴埋めになる可能性があります。
下から3行目で同時分布の形が変わっていますが、これはなぜですか?
これは変数変換を行なっていますが省略しすぎましたね。詳しい変換の内容を載せますね。
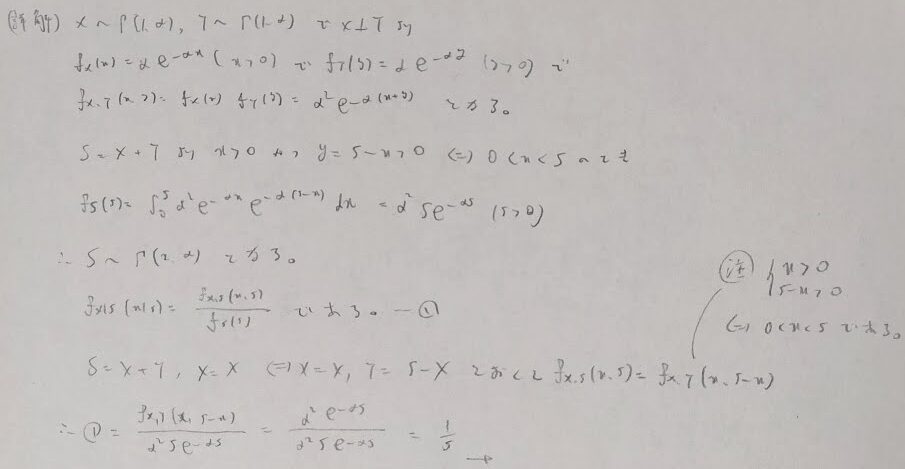
平成6年度数学Ⅰ問1(4)標準正規分布
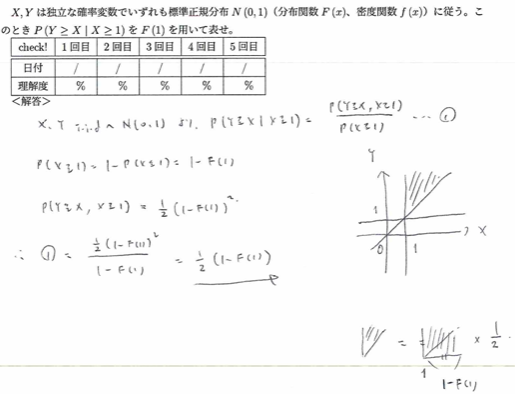
面積で考えます。条件付き確率の定義通り考えないとミスをしますのでご注意ください。
この問題も本番でこのようなうまい方法を思いつけるか?と言われれば難しいと思います。そのため下記に正攻法を書いておきます。
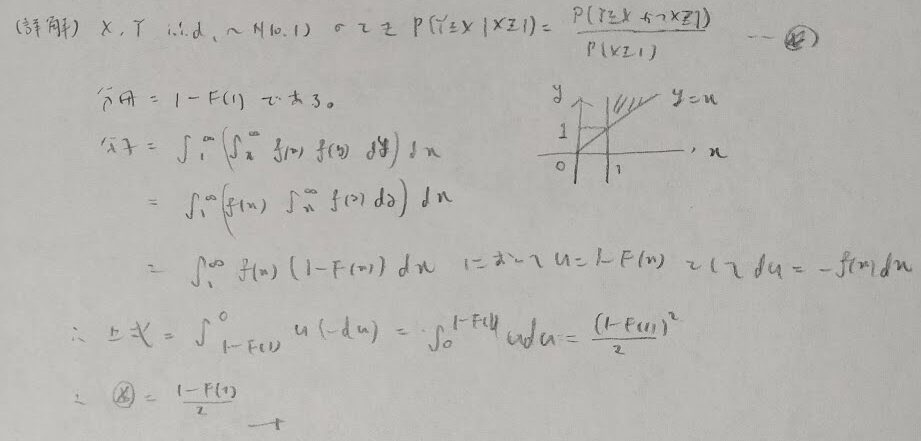
平成22年度問2:就職問題


平成29年度問1(1)工場生産

XとYの設定が全てです。かなり良い問題です。
2019年度問1(2)3つの点

条件付き分布の考えをしっかりと用いる良問です。
本問では一様分布の期待値および分散の公式を駆使します。覚えていないと時間切れになるので確実に反応できるようにしておきましょう!
2020年度問2:クイズ問題(最難関)
本問は大問2で最難関の問題です。取れる問題だけ復習できれば十分です。



とてつもない処理量で歴代の大問2で最難関です。
2022年問1(2)コイン投げ

難問です。うまく前の問題の結果を用いることを考えましょう。難所は(2)の組み合わせの部分で、3変数を2変数に直して少しだけ実験すると組み合わせの式を立式できることがわかります。
混合分布
平成24年度問1(4)細菌

パラメータの中に更なる確率変数がある場合を混合分布と言います。後の複合分布とは異なるものです。
本問の積分区間は問題文よりaもxも正の数全体であることに注意しましょう。
複合分布
本記事のメインの部分です。ここが分かるかどうかが合否を分けるポイントとなります。
平成元年度数学Ⅰ問1(7)入院患者数

複合分布の問題は大問の穴埋めでも出る可能性があるので、別解の最短の方法と上の理屈から考える2つのパターンに習熟しておくことをおすすめします。
この別解の方法はポアソン分布の再生性の応用的な考えでも納得がいく結果ではないでしょうか?
平成元年度数学Ⅰ問3:2の指数

複合分布で困ったら変数の取りうる範囲を考えると先に進めることが多々あります。また本問こそkの取りうる値を考えることが本質的です。幾何分布の深い理解や級数計算のテクニックも要求される難問です。
平成4年度数学Ⅰ問3:分布関数

分布関数に関して、複合分布の考え(条件付き確率の考えから派生します)を用いるのが本質です。
2025年11月現在、本問題の類題は出題されておりません。そのため大事な問題となります。
平成6年度数学Ⅰ問3:誤植問題

難問ですが以後未出の問題です。狙われる可能性が高いので習熟しておきたいところです。
とことん難しくしてやろう!という最近のような製作者の意気込みを感じます。当時の受験生も大変だったでしょうね。
平成8年度数学Ⅰ問1(4)複合分布の分散

エンベックス+べネックス2乗と覚えましょう。
平成9年度数学Ⅰ問1(3)産卵

確率変数の分解を行うと納得のいく結果です。
この問題について、下記に公式を使わない複合分布の考えに基づいた導出を行なっておきます。
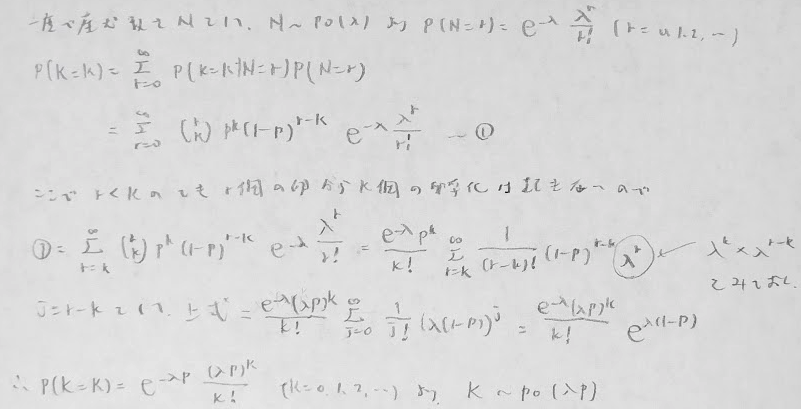
平成11年度数学Ⅰ問1(6)男の子がいる確率

別解の公式を知らないと難問です。
条件付き期待値の意味とタワーの法則
全期待値公式
まずは基本的な条件付き期待値の性質をまとめます。
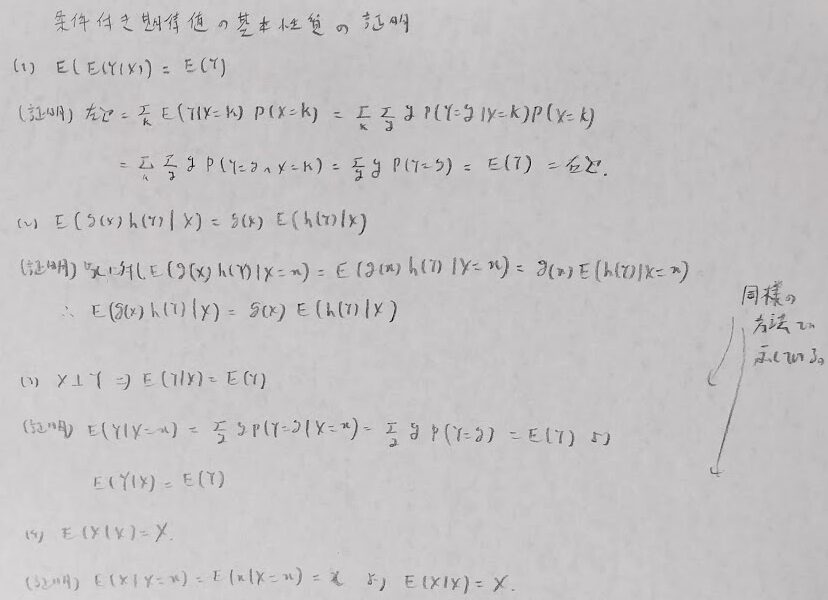
全分散公式
混合分布の性質も証明しておきます。その際に全分散公式を用いるため、この後に証明を行います。

全分散公式の証明も行っておきます。
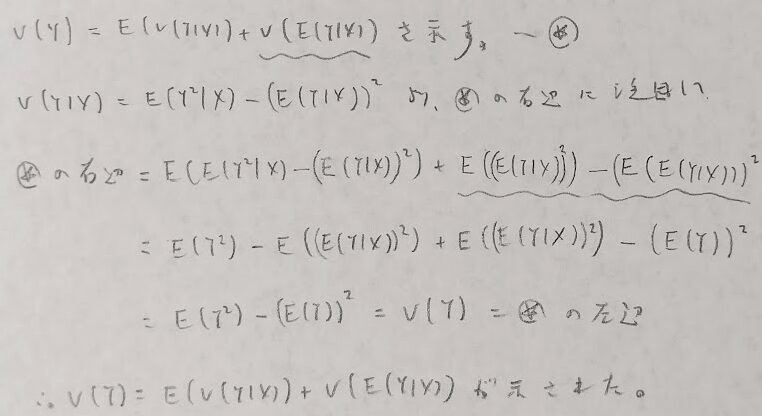
混合分布の具体例
次に混合分布の具体例を紹介します。
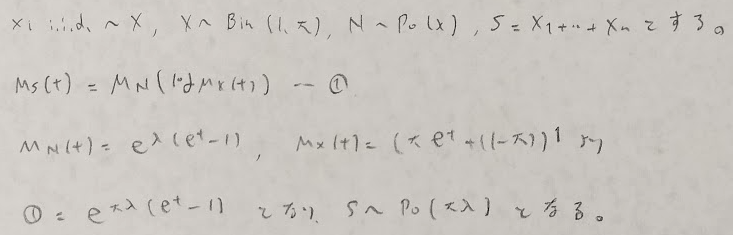


タワーの法則
タワーの法則というものがあり、アクチュアリー数学では未出ですが知っておくと便利です。
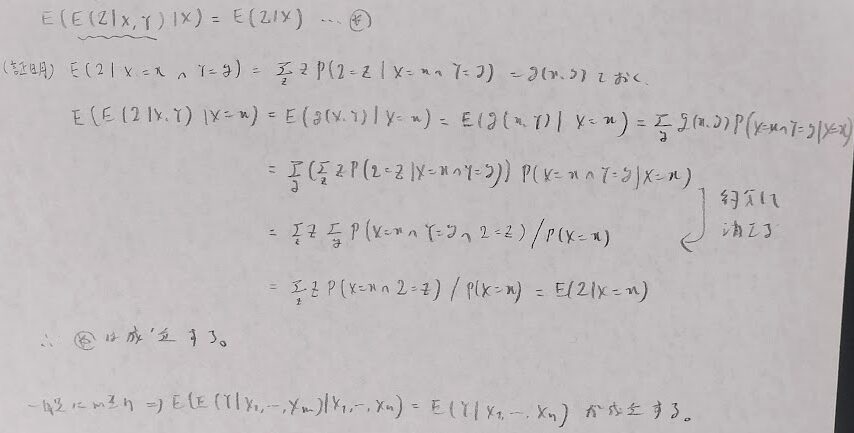
無記憶性の利用
最後に時短テクニックを紹介します。ただしポアソン分布には無記憶性がないことに注意をしてください。
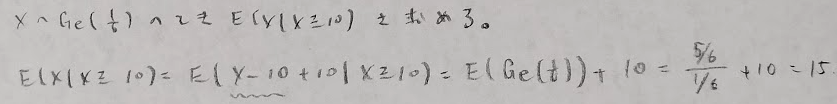
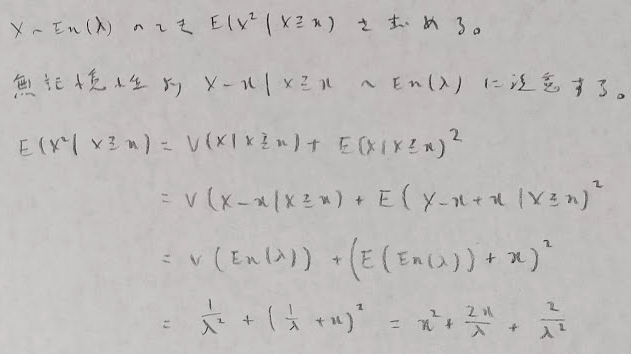
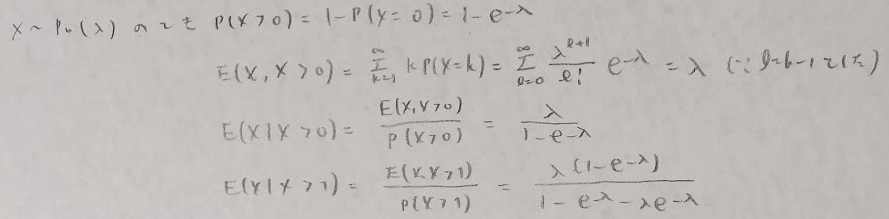
また条件付き確率の役割としては、Xの関数g(X)の中でYとの平均2乗誤差を最小とするときのg(X)がE(Y|X)です。
『アクチュアリー試験 合格へのストラテジー 数学 第2版』は合格に必須の公式が掲載されている唯一の参考書です。お手元に置いて本記事をご覧くだされば学習効率が上がります。本書に載っている複合分布の公式は要確認です!