本記事ではアクチュアリー数学の過去問において、離散型確率変数でも連続型確率変数にも分類されにくい一般的な確率の問題を扱います。そのため難易度は高くなります。
このようなタイプの問題は初見率が高いため、必然的に難問になる可能性が高まります。
本記事を学習される前に、次の2つの記事の復習をお勧めします。
本記事ではアクチュアリー数学で使われる特殊な公式を多々用いています。『アクチュアリー試験 合格へのストラテジー 数学 第2版』は合格に必須の公式が掲載されている唯一の参考書です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
また本章では特殊な確率の題材を問う問題が頻出です。合格者が推薦する『明解演習 数理統計』との併用をおすすめします。本書と同じ問題が出ているためです。
確率
平成元年度数学Ⅰ問1(6)チェビシェフの不等式

別解の方は公式の解答ではなく自力で解いた解法になります。しかし別解の方がストレートな感じがしますので、本番では別解の方が速く正解に辿り着けます。
平成2年度数学Ⅰ問1(2)碁石の問題
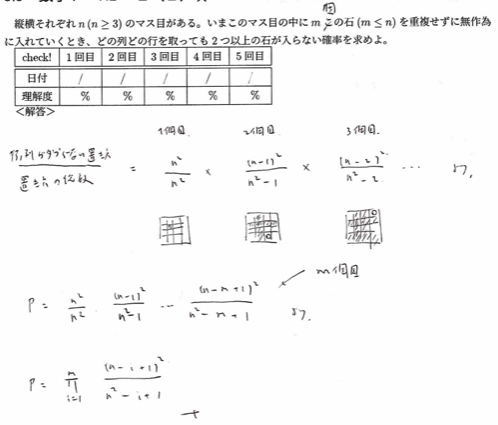
かなり特殊な問題です。2025年11月現在、これ以降は試験で問われていないタイプです。
平成3年度数学Ⅰ問1(9)1ダース問題

余事象の確率がテーマの良問です。
ケース3では2/3だと思いました。どこが間違っているのですか?
不良品が入っている箱をAまたはBとします。どちらかに不良品が入る可能性は(問題文では与えられていませんが)1/2です。対称性よりAでもBでも確率は1/3なので、結局答えは1/3です。
平成7年度数学Ⅰ問1(4)確率密度関数となる確率

一体どこから手をつければ?!という難問ですが、ヒントはあります。それは確率密度関数の定義を思い出すことです。
困ったら定義に帰りましょう。原点回帰です。
また、本問はラプラス分布を知らないと解けません。
もしラプラス分布に気づかない場合(多分こちらが普通です。僕も2024年の受験時には気づきましたが2025年の今は気づかなかったです)は素直に全確率=1からβとαの関係を下記のように求めましょう!
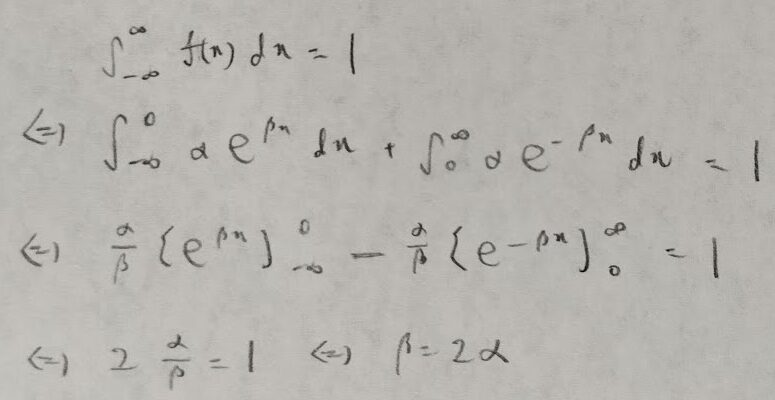
平成7年度数学Ⅰ問2:宝くじの問題

最後の問題が難問です。今後出題される可能性があります。
平成10年度数学Ⅰ問1(6)出火確率

『明解演習 数理統計』に全く同じ問題があります。本書の確率分野の有名問題は要チェックです。
試験に未出の問題がまだたくさんあります。
例えば今回のこの出火問題の類題として次のようなパターンもあります。
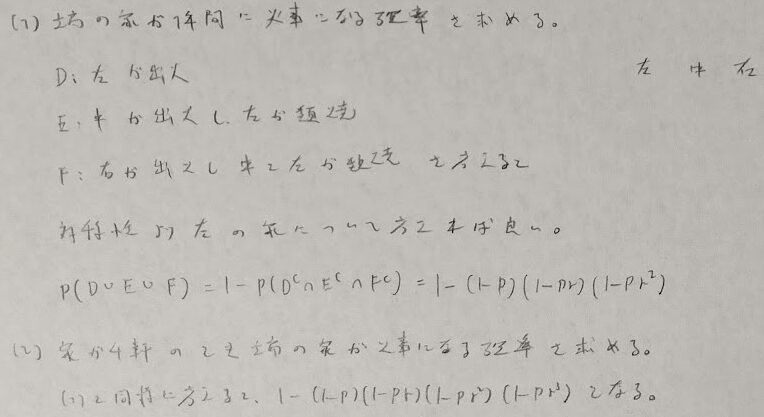
平成11年度数学Ⅰ問1(5)重複組み合わせの応用

これは瞬時に解きたい問題です。
平成13年度問1(9)トレーズ

超有名問題です。『明解演習 数理統計』に数字のみが異なる問題が載っています。
本問は撹乱順列の問題です。撹乱順列をn!で割ったものが先ほどの公式です。撹乱順列の総数は3項間漸化式の立式か、包除原理で求めます。前者は特定のi番目が1番目に置換する場合と、特定のi番目が1以外に置換する場合は排反であることから漸化式の立式が可能です。後者は余事象を考えます。i番目が移動しない順列の総数をAiとでも設定すると全体の置換数n!からn個の集合の和集合を引けば良いです。
言葉だけでは伝わりづらいので数式で導いてみます。
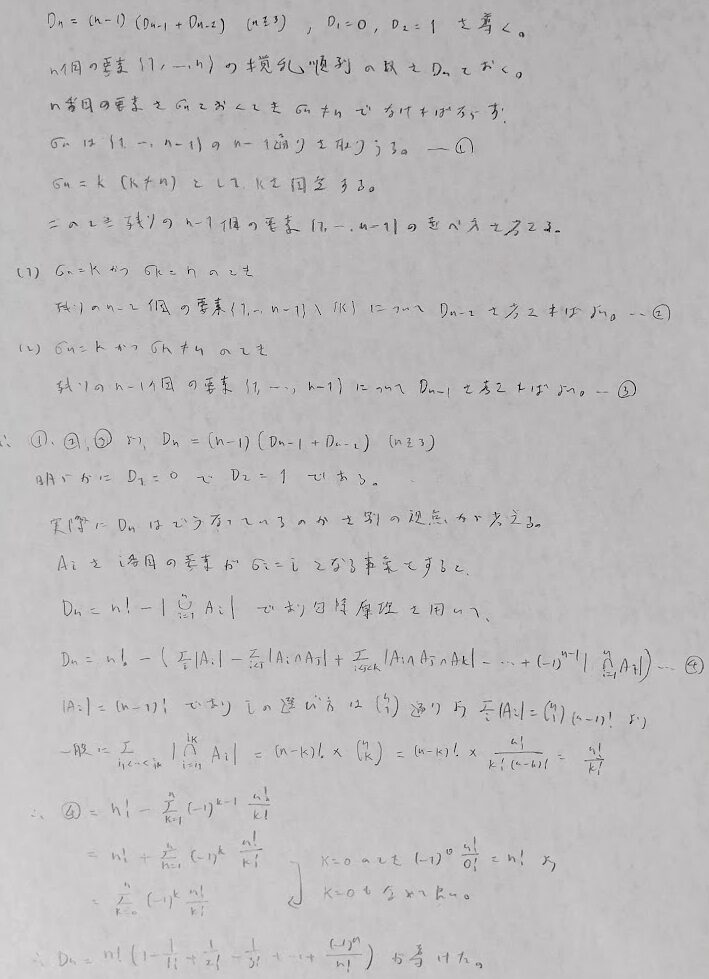
平成14年度問1(3)レアな問題

本問はかなり特殊なタイプの問題です。シグマを使うことに気がつかないと泥沼です。
平成14年度問1(8)無限小数

無限小数の問題は繰り返しを意識した方程式の立式を考えます。
式が簡略化されていて分かりませんでした。もう少し行間を広げてください!
了解です。P=(1/6)×(1/6)+(1/6)×(1/6)×(2/6)+(1/6)×(1/6)×(1/6)×Pです。
平成16年度問1(3)ひっかけ問題

前半部分で1つの場合を引くことに注意しましょう。
平成29年度問1(2)2次元ランダムウォーク

本問で与えられているΣの公式は覚えておきなさいというメッセージかも知れません。
本問で用いた公式はヴァンデルモンドの恒等式というものの一種です。これを紹介し導いておきます。
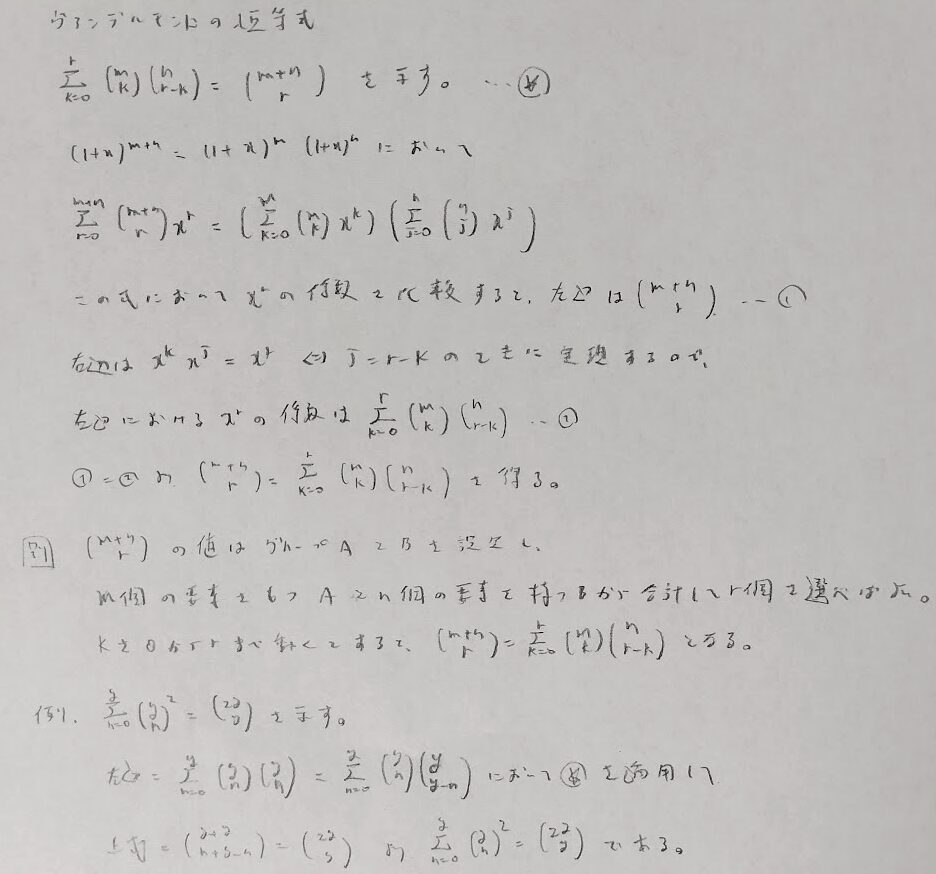
これは超幾何分布のところで出てきた内容と本質的に同じものですね!
期待値
平成7年度数学Ⅰ問1(3)イヤリング問題

確率変数の設定を意識しましょう。
イヤリング問題は初見ではかなり厳しいですね。
平成9年度数学Ⅰ問1(9)玉ねぎ型確率

平成15年度問1(6)最初の立式

2018年度問1(1)正誤問題

最後の独立と無相関が同値でない反例はX~U[-1,1]でY=X^2とおくと明らかにXとYは独立ではないです。しかしCOV(X,Y)=E(XY)-E(X)E(Y)=E(X^3)-0E(Y)=0となります。
2020年度問1(1)赤玉と白玉

確率変数を複数設定するので難問です。類題は未出のため要チェックの問題です。
2024年度問1(1)最初の出方

分散
平成5年度数学Ⅰ問1(1)何から手をつけたら良いか不明の問題

難問です。とにかく解法を頭に叩き込むしかありません。
平成10年度数学Ⅰ問1(7)確率変数の分解

分散のところで共分散が必要なことに気づけば間違うことはないでしょう。
2018年問1(4)コイントス

二項間より離れた箇所での共分散は0であることに注目します。素晴らしい良問ですが難問です。
相関係数
平成3年度数学Ⅰ問1(7)二変数関数

かなりの計算量を要求される統計検定1級の統計数理に似た感じの難問です。
平成11年度数学Ⅰ問1(8)回帰分析

かなり良い問題だと思いますが、頻度は低いです。どちらかというと統計検定1級の統計数理で出そうです。本問のように恒等式系の考えはとても大事です。
本記事ではアクチュアリー数学で使われる特殊な公式を多々用いています。『アクチュアリー試験 合格へのストラテジー 数学 第2版』は合格に必須の公式が掲載されている唯一の参考書です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
また本章では特殊な確率の題材を問う問題が頻出です。合格者が推薦する『明解演習 数理統計』との併用をおすすめします。本書と同じ問題が本番でも多数出題されています。