アクチュアリー数学の過去問で連続型確率分布の問題を解説します。離散型確率分布の問題はこちらで扱っています。
本記事ではアクチュアリー数学で使われる特殊な公式を多々用いています。『アクチュアリー試験 合格へのストラテジー 数学 第2版』は合格に必須の公式が掲載されている唯一の参考書です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
正規分布
1変量正規分布を扱います。頻度は高くないですが条件付き分布の例題を紹介します。
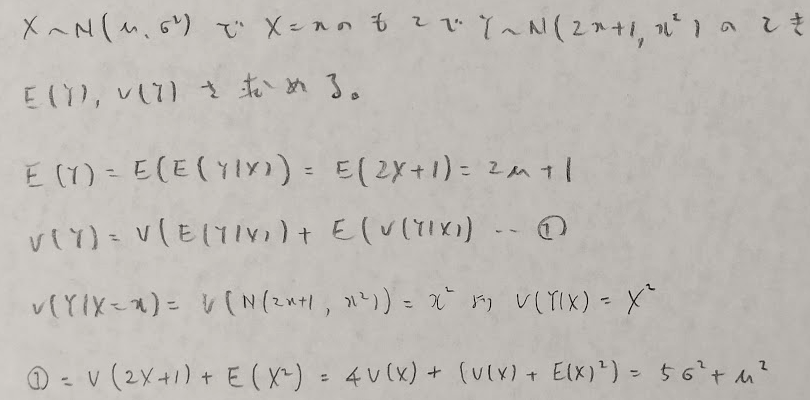
直交変換ではn変数の積率母関数は不変である事実は覚えおきましょう。計算を省くことができます。
昭和63年度数学Ⅰ問1(2)正規分布の確率密度関数

何回か類題が出題されている典型問題です。時間を時間をかけることなく最短で解けるように練習しておきたい問題です。
平成2年度数学Ⅰ問1(9)標準化

そのまま計算するのではなく、標準正規分布化できないか?という考えが大切です。
平成3年度数学Ⅰ問1(6)標準正規分布の絶対値の期待値

即答できるようにしておきましょう!
平成10年度数学Ⅰ問2:正規分布の分布関数

区分求積法のように長方形で不等式評価をしていきましょう。困ったらロピタルの定理も使いましょう。
平成21年度問1(5)ガンマ関数とベータ関数の利用

途中でパレート分布を持ち出していますが、試験場で思いつくのは至難の業です。素直にガンマ関数とベータ関数の利用を考えましょう。
指数分布
平成9年度数学Ⅰ問1(4)記憶保持平均時間

どこから手をつけるか困ったら、Xが従う確率密度関数においてパラメータの設定をしてみましょう。
2021年度問1(2)通話料金の期待値

本問は期待値の式の立式→極限計算という二段構えでかなりのボリュームです。E(g(X))となる関数g(X)を求めようとするところが一番の難所です。
ガンマ分布
昭和62年度問3:ガンマ分布

ポアソン分布のパラメータの区間推定で登場した精密法に関連する問題です。
平成2年度問4:ガンマ分布の公式

この問題はとある公式を知っていれば1分以内で正解にたどり着けます。上の本に詳しく載っていますが、下記記事にも証明も入れつつ解説をしていますのでご覧ください。
平成13年度問1(6)積率母関数

公式を知っていれば1発の問題です。しかしアクチュアリー数学では他にも覚えることがあるので、本問の公式は後回しにしてもOKです。実際、簡単な期待値計算で算出することが可能です。
平成19年度問2:稼働停止

ガンマ分布の意味を問われている良問です。今後、類題の出題もあり得ます。
パラメータ1の指数分布の最小統計量は、n個の指数分布の和で表されます。
ラプラス分布
平成元年度数学Ⅰ問1(2)積率母関数

実際に出題された場合は素直に計算したほうが良いですが、本問を選んだ理由は指数分布との関連性にあります。
本問でのポイントはパラメータλの指数分布の差がパラメータλのラプラス分布になるということです。
カイ2乗分布
平成5年度問4:公式利用

これぞアクチュアリー数学というべきテクニカルな問題です。
ディリクレ分布
平成9年度数学Ⅰ問1(2)係数比較

確率密度関数の形からディリクレ分布をひらめけるようにしましょう!
平成18年度問1(1)相関係数

周辺分布の公式は覚えておきましょう。また期待値計算の際はディリクレ関数を持ち出すことが大事です。
多変量正規分布
ここは難易度が高いので上記の本からの抜粋として簡単な例題をまずは紹介します。
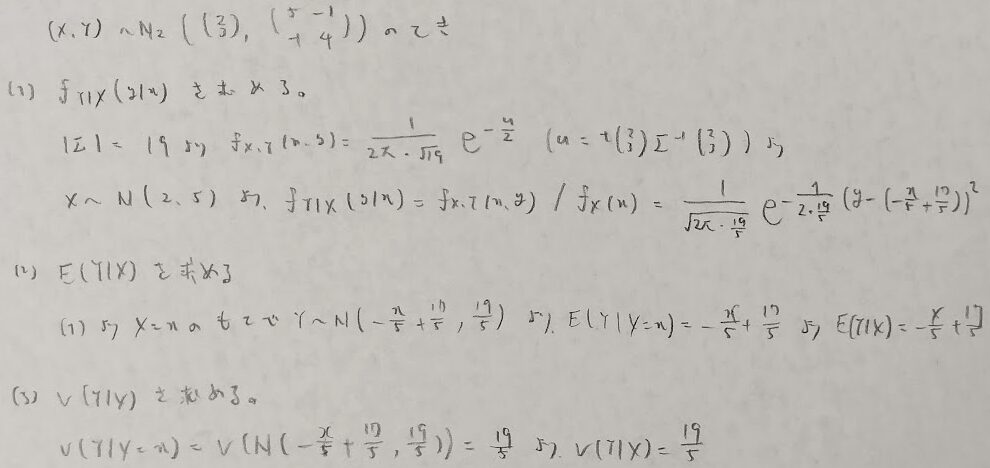
平成29年度問2:指数分布との関係


本問は前半は答えから逆算して埋められる箇所が多いですが、後半は難しいです。
指数分布の積率母関数や、ガウス積分の公式など知っていないと時間内に処理不能となる難問です。
多次元ベータ分布(ディリクレ分布)
アクチュアリー数学の過去問としての出題はありませんが今後の出題の予想としてテクニック的な問題を掲載しておきます。
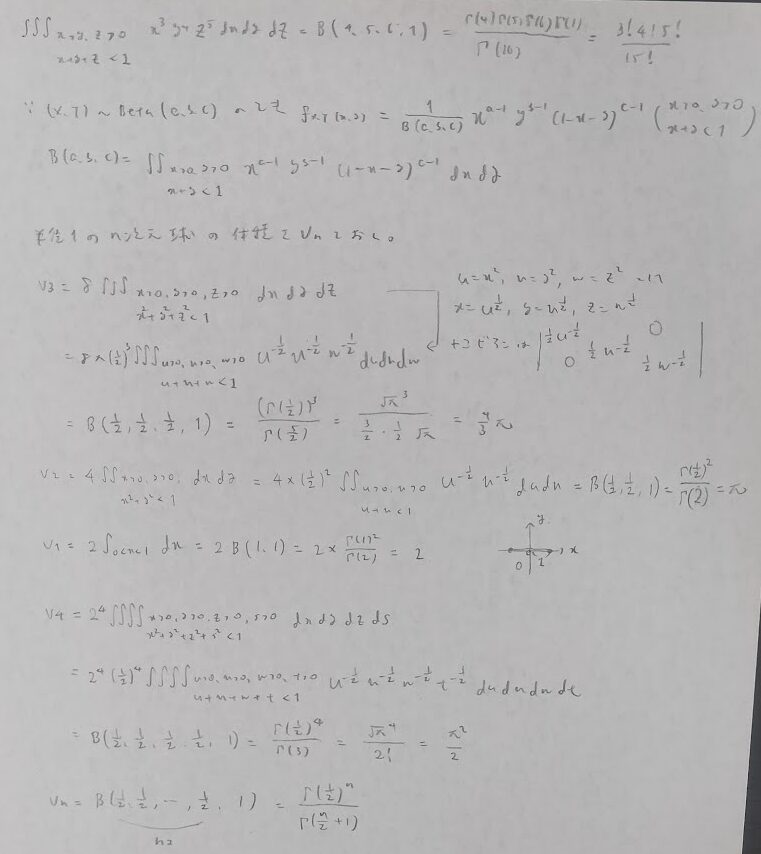
一様分布
平成8年度数学Ⅰ問4:一様分布最難関

とても難易度が高い問題です。
その他の連続型確率変数
平成4年度数学Ⅰ問2:重積分

結構な盲点です。
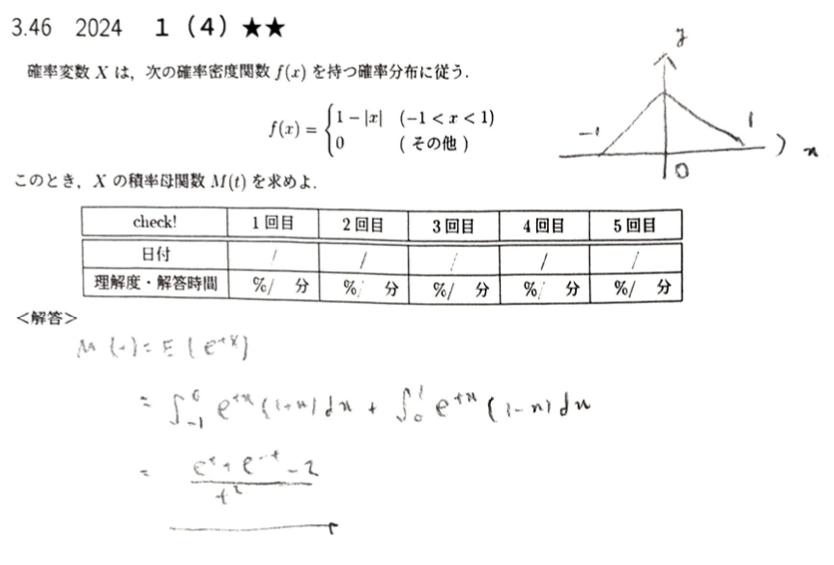
2024年度問1(4)積率母関数
死力・故障率・危険率
連続分布の応用として死力(故障率・危険率)の問題を『弱点克服 大学生の確率・統計』を題材に解いてみましょう。
対象となる分野によって呼び方が異なるのですね!
次の問題を通して生存関数→死力→生存確率→平均余命の流れをおさえましょう!

本記事ではアクチュアリー数学で使われる特殊な公式を多々用いています。『アクチュアリー試験 合格へのストラテジー 数学 第2版』は合格に必須の公式が掲載されている唯一の参考書です。お手元に置いて本記事をご覧くだされば学習効率が上がります。