アクチュアリー数学で出てくる回帰分析の過去問を解説します。大まかな構成は、線形回帰と非線形回帰です。前半は重回帰分析などで、後半はロジットモデリなどです。後半ではロジットモデルやプロビットモデルには該当しない一般のモデルも扱います。近年では2022年に指数関数モデルが出題されました。今後このような問題が登場する可能性が高いです。
アクチュアリー数学のモデリングの内容では最も基本的な内容になります。ここでしっかりと得点を取りましょう!
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
単回帰
平成5年度問1(3)標本相関係数など

上から3行目の式も一応公式ですので、覚えておきましょう。
xとyが逆になった時に処理しやすい式ですよね。
平成20年度問1(9)誤差分散
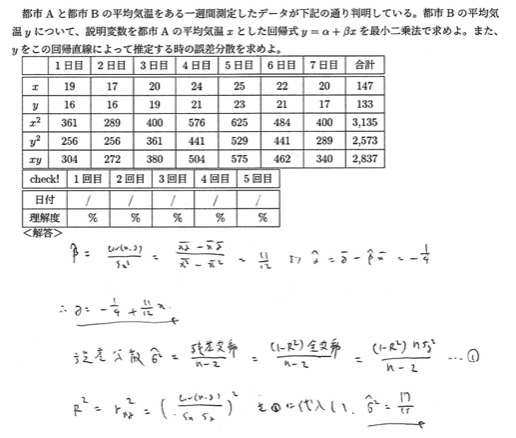
単回帰分析では、誤差分散の分母は残差変動の自由度であるn-2で、残差変動を割った値になります。自由度については、、全変動の自由度がn-1で回帰変動の自由度が1(独立変数はxのみの1つ)を引いたn-2となります。
平成27年度問1(9)多変数
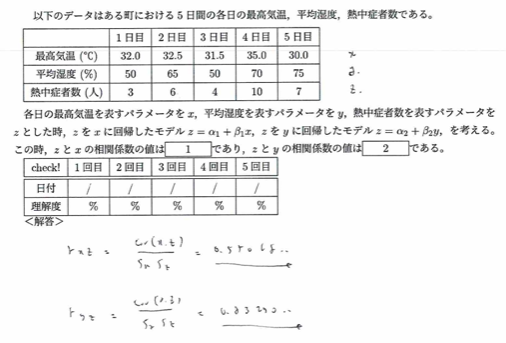
何が独立変数か?をしっかりと読み取りましょう!
平成28年度問1(9)決定係数

統計検定1級の問題レベルに近いです。決定係数を求めるところが難しいです。
重回帰
昭和63年度問1:公式の応用

パッと出てくるのは最初の正規方程式のみです。あとは計算で処理します。
平成19年度問1(9)典型問題

本番の試験でもこのような問題だったら嬉しいのですが(笑)
平成25年度問1(10)定数項ダミー

適宜、別解を用いる方が良いです。穴埋めでも出題される可能性があります。
2020年度問1(9)係数ダミー
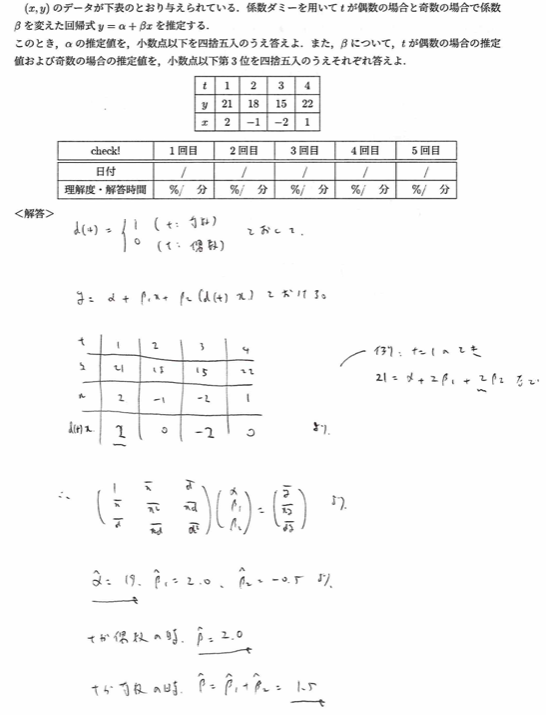
第2行の式を作れるようにしましょう。定数項ダミーよりも難易度は上です。
2024年度問3(1)デザイン行列

2021年度問1(10)多項式モデル
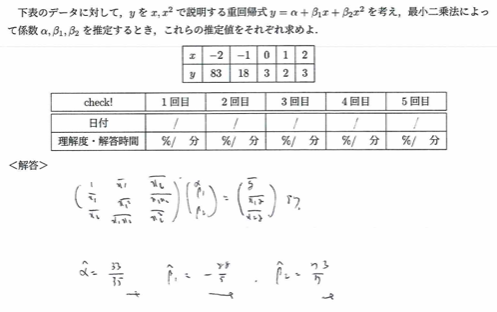
これらの問題のバリエーションは『データ解析のための数理統計入門』に詳しく例題とともに書かれています。
非線形回帰(ロジットモデル)
平成21年度問1(10)ロジットモデル

yからy’への変換式つまりロジットを出すことを意識しましょう。
非線形回帰(プロビットモデル)
平成29年度問1(9)プロビットモデル

非線形回帰(ロジットモデルとプロビットモデル以外)
平成17年度問1(5)変化球

2022年度問2(4)指数関数モデル

どれもxとy’の値を表にまとめてから正規方程式の公式に代入する流れは同じです。他の問題は下記の書籍で取り組みましょう!
全体的なおすすめの公式・問題集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。






