本章ではアクチュアリー数学の標本分布論+下記記事に該当しない総合問題を取り扱います。
アクチュアリー数学ってとても範囲が広いですね。
そうですね。だからこそ難関資格として通用しています。今回も頑張りましょう!
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
標本分布論
平成4年度問1(2)共分散
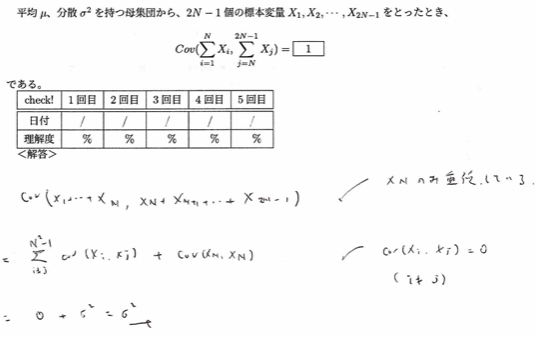
有限母集団の指定がない限り、つまり無限母集団からの標本を考えた際の共分散は0です。つまり独立なので無相関ということです。
なかなか面白い問題です。分散との違いを意識しましょう。
平成28年度問1(5)歪度のような式

とにかく色々なことに気づかないと最後まで行き着けない難問です。
平成28年度問3:ガンマ分布と一様分布

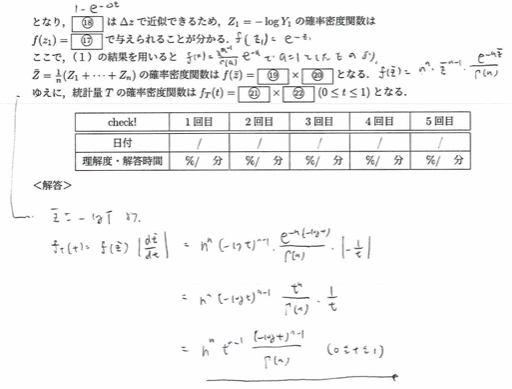
(1)の最後はかなり特殊なタイプです。(2)は今回が初見の問題です。以後未出なので今後狙われる可能性大です。
全体的にかなりギミック的な問題ですね。
確率統計分野の総合問題
昭和63年度問3:相関係数

超有名問題です。
平成3年度問1(5)ベイズ推定値

積分範囲は座標平面にグラフを書けば判明します。
統計検定1級では頻出ですがアクチュアリー数学では意外と出ていませんので、今後狙われる可能性大です。
平成8年度問1(5)推定量

平成10年度問1(4)分散の最小値

2023年度問2(1)メジアン
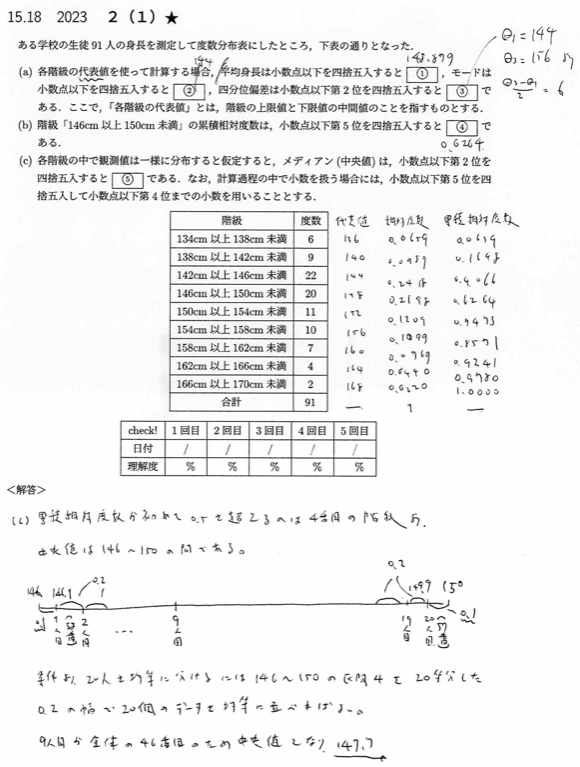
直感的には中央値の順位が91/2=45.5より、答えは146+4((45.5-37)/20)=147.7です。
最後の設問を解く際は、「等分に分ける」ことを徹底します。本番で解いた時は時間制限内では方針がわからずにいました。試験本番で困ったら基本に立ち返る勇気が大切です。
以上でアクチュアリー数学の統計分野を終わります。
とにかく統計的検定の話題が占めていましたね。難しいですが得点源にできるように頑張りましょう!
アクチュアリー数学の全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。