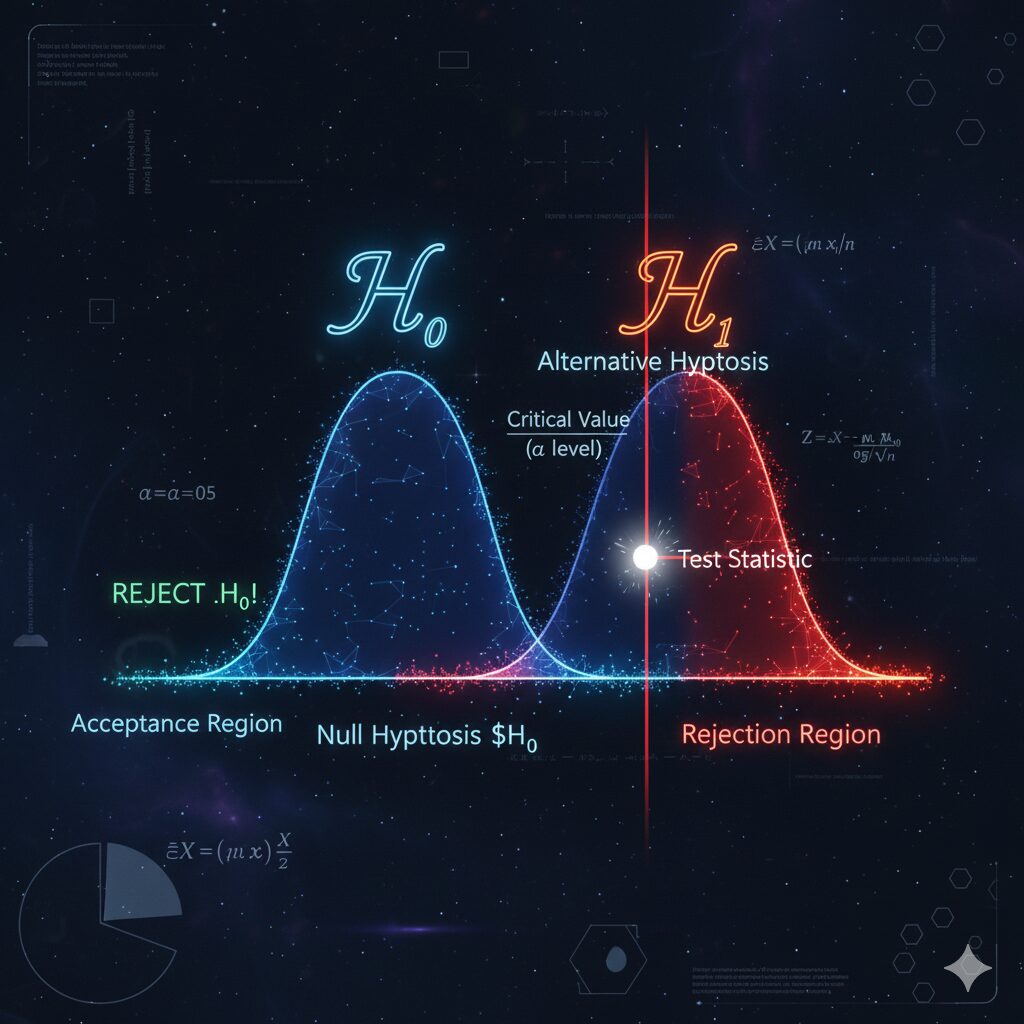
本記事では検定の過去問を体系立てて解説します。点推定の章よりも遥かに多い問題数になりますので、事前準備として区間推定の理解が必要ですので未学習の方は下記記事をご覧ください。
検定の内容が、アクチュアリー数学で最頻出分野です。しっかりと学習をして合格を目指しましょう!
本記事は検定の内容を扱いますが、第1種過誤の確率の問題などカテゴリー別に分けてわかりやすく問題を整理して解説をしていきます。下記の参考書を片手に頑張りましょう!
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
アクチュアリー数学では第1種過誤と第2種過誤の問題が圧倒的に多いです。ここで混乱していると得点チャンスを逃すことになりますので、しっかりと学習をしていきましょう!
母平均に関する検定など正規近似を用いる場合(ウェルチの検定以外)
平成4年度問3:母平均に関する検定

F検定は通常は右側検定になります。
基本的に等分散性の検定→分散をプールした母平均の差の検定を行う流れです。等分散性が満たされない場合は後述のウェルチの検定の出番になります。
平成6年度問1(1)母比率

頻出問題ですので、しっかりと正解したい問題です!
平成9年度問1(3)返信率

返信率は母比率の問題として考えます。また大標本であることにも注目しましょう。
母分散比に関する検定
2024年度問2(4)F検定

平成3年度問1(4)どちらを分子にするかの判断

F検定のベースは不偏分散です。不偏分散か標本分散かの違いに注意です。
平成3年度問2:典型問題

典型問題ですが難易度は高いです。近年の小問集合に頻出のタイプです。混乱をしないように練習しておきたい問題です。カイ2乗分布を作り出すことがポイントです。本問は年度を追うごとに他の問題タイプとの融合が始まります。ベーシックなタイプの本問をしっかり解けるようにしておきたいですね。
平成10年度問3:分散に差があるか

分散に差があるか?と言われたら等分散検定を行います。
(3)は良問です。2025年11月現在、類題は出題されておりません。
平成13年度問2(9)z値

標準正規分布ではz値の絶対値が3に近づいたら、上側確率はほぼ0になります。すなわちz値が±3より外れる可能性は極めて0であると言えます。
ある値離れたという表現は+の場合とーの場合を考えるのが定石ですが、対称性より一致することがわかります。そのため解答では+の場合のみ考えています。
典型問題と思いきや、かなりの良問でしたね。
平成26年度問1(7)意地悪問題

注がすべてです。ここを読めないと解けません。
第1種の誤りと有意水準と第2種の誤りと検出力
昭和62年度問4:検出力関数

かなりの変化球タイプですが、本質は中盤の統計量が分散1の正規分布に従うことを見抜くことです。
平成元年度問1(9)(10)検出力最大

右側検定の棄却域はある値よりも大きいということです。まずは棄却域を設定しましょう!
平成3年度問1(3)第二種過誤の確率

基本問題ですが、それぞれの過誤の意味を把握するのに最適な良問です。
2024年度問2(3)コイン問題

平成4年度問1(3)最良の検定方法

有意水準の条件のもとで、検出力が最大となる検定が良い検定です。
平成7年度問1(2)混合問題

まず棄却域の設定をしましょう。検定問題でわからなくなったらこの方針が鉄則です。
平成7年度問1(5)順序統計量

ひっかけ問題です。最後の最後にお気をつけください。
平成9年度問1(1)変化球

重積分するのは同時分布ですのでご注意ください。基本的ですが焦ると処理不能になります。
非常に良い問題です。2025年11月現在、類題の出題はありません。
平成9年度問2:抜取検査(最難関)

類似問題の中では最難関です。とても複雑な設定なので、帰無仮説と棄却域の設定をしっかりと行いましょう。96%以上と言えるか→96%であればOKなので対立仮説を96未満とするなどの考えが大事です。(2)では対立仮説を96未満と設定していきます。
平成10年度問1(1)典型問題

平成10年度問1(2)対立仮説

対立仮説が分かりにくいので、やや難しいですが2025年現在のレベルでは基本問題です。
平成11年度問1(2)棄却域と検出力最大

検定統計量Xの標本平均を用いて、検出力が最大となる棄却域(一様最強力検定)は、ネイマン・ピアソンの補題により、対立仮説 H1の方向で有意水準 αを満たす領域です。
よく考えれば当たり前の問題です。
答えよりも大きくしようとすると、検出力が減ってしまいますし、答えよりも小さくしようとすると有意水準そのものが変わってしまいますね。
平成19年度問1(6)玉取り

確率計算の分子に注意しましょう。
平成29年度問1(7)分析問題

問題文から帰無仮説をこのように設定できるか?が勝負の分かれ目です。やや意地悪な書き方だと感じます。
ここら辺が検出力系の問題の最高到達点です。問題の内容的にQC検定1級の内容に近いです。しかしこれ以上難しくすると試験にならないと判断にしたのか、今後は違った方向性で難易度を上げています。
2018年度問1(7)負の二項分布

ただただ計算が面倒な問題です。2025年11月現在、類題は出題されておりません。一般的に負の二項分布を考えつくことは難易度が高いです。
2019年度問1(8)変化球
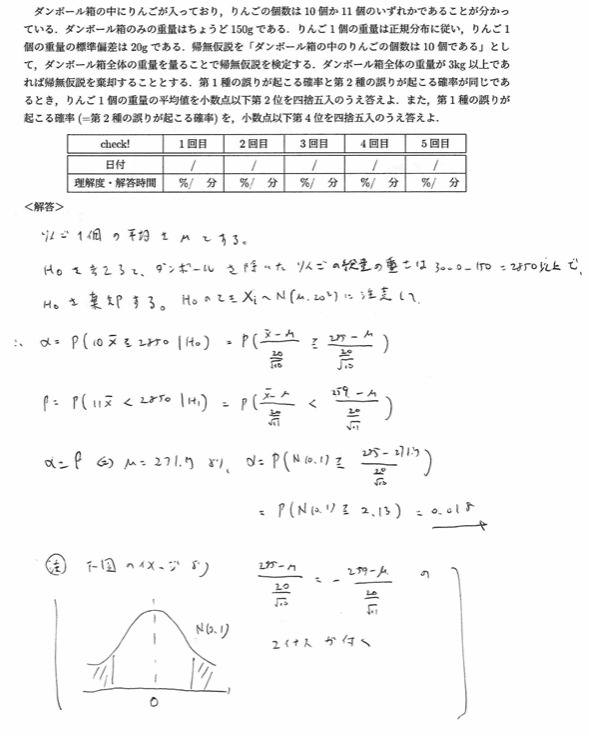
母平均を設定する必要がある良問です。とても素晴らしい問題です。2025年11月現在、類題は出題されていません。
2020年度問1(7)変化球

小問のレベルがどんどん上がっていきますね。
2020年度問1(8)検出力の表現

検出できますよ=「棄却域に入るので異常ですよと言えますよ」ということです。
2022年度問2(2)棄却域

2022年度はアクチュアリー数学最難関の年です。本問は棄却域の設定で最も難易度が高い難問です。
適合度検定
平成6年度問3:正規分布

計算が厄介なだけですが、未知母数がないことに気をつけましょう。
平成11年度問3:プール後の計算

λの最尤推定値は、180/75で計算しています。つまり1日あたりの平均的な苦情件数を求めていることになります。これがパラメータλの推定値とします。
平成20年度問3:証明問題

厄介なのは尤度比検定の(6)の計算のみで、あとは知っている語句を入れていくだけの作業です。
2023年度問2(4)メンデルの法則

僕が実際に受けた2023年度の回です。時間がなくて解けませんでした。アクチュアリー数学は試験時間が3時間ですが全然時間が足りません。ちなみに2024年度の回では不合格Ⅰつまり合格まであと数点でした。この時も時間の足りなさを感じました。
独立性の検定
平成2年度問3:独立性の検定

平成21年度問1(8)効果があるとは

独立性の検定を用いるための文言に注目しましょう。
平成25年度問1(9)自由度

独立性の検定の自由度は本問では(2−1)(3−1)=2です。もしも適合度の検定なら、6−1(未知母数がない場合)=5になります。
2018年度問1(8)イェーツの補正

イェーツの補正を行うとカイ2乗統計量の値を小さくすることになり、棄却されにくくなるわけです。

相関係数に関する検定
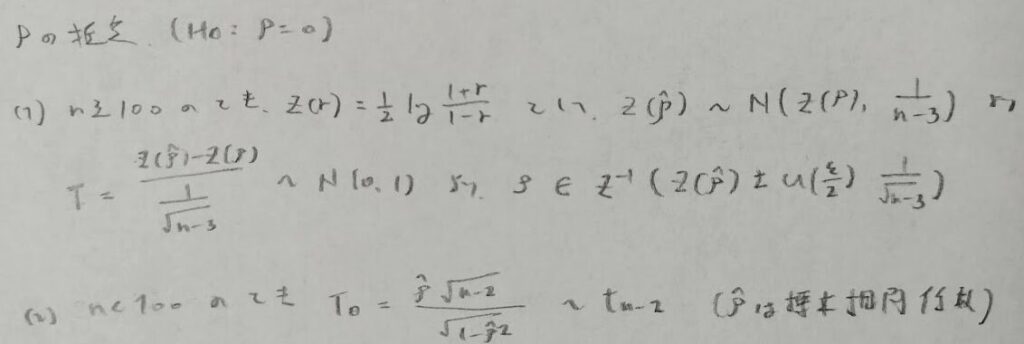
平成5年度問2:小標本の場合

メタ的ですがz変換表がない時点で小標本の場合だなとわかります。
本問は統計量Tに関する公式を知らないと解けません。『アクチュアリー試験 合格へのストラテジー 数学 第2版』に載っている公式をしっかりと覚えましょう!
2021年度問1(8)z変換

相関係数に関する検定問題は出題歴がほぼないのですね。
これは2025年度の試験で出そうですよ!笑
総合問題
平成13年度問3:指数分布

(1)は式の形から指数分布だと分かりますし、パラメータはそのままKとなります。(2)は区間推定の応用になります。
平成23年度問1(7)指数分布

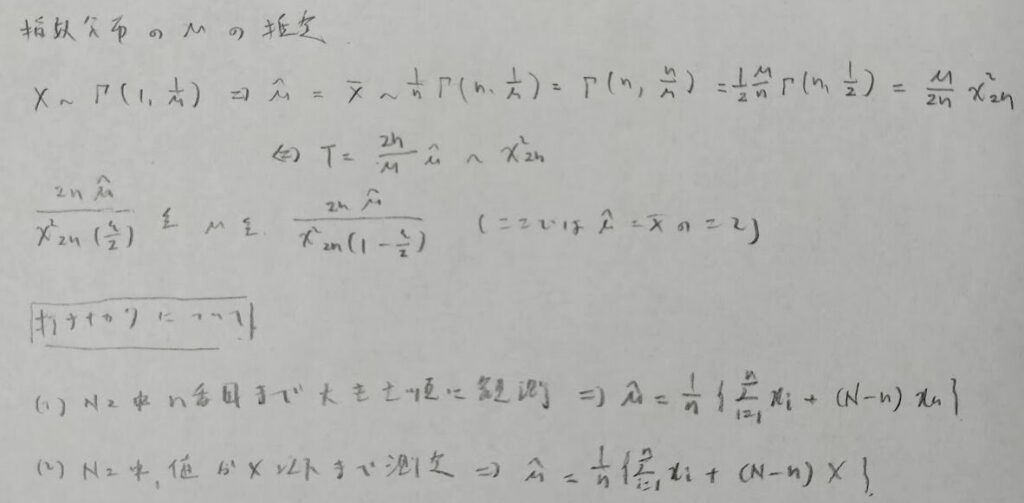
2023年度問2(3)指数分布

今までに登場した難問的なものが融合されてしまった問題です。2022年度の難易度が上がりすぎてしまったため、このような形での難易度の上げ方になったと思われます。今後もこの傾向が続くでしょう。
平成22年度問3:ポアソン分布に関する精密法

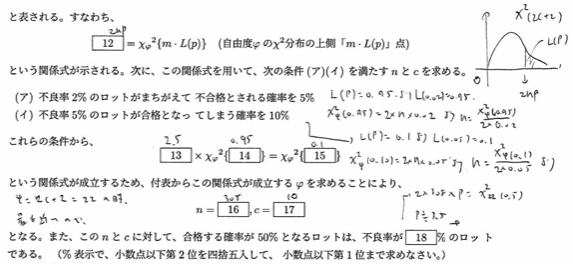
QC検定1級の抜取検査に関係するとても難しい問題ですが、2025年度のアクチュアリー数学で狙われると考えています。(2025年11月現在の考察)
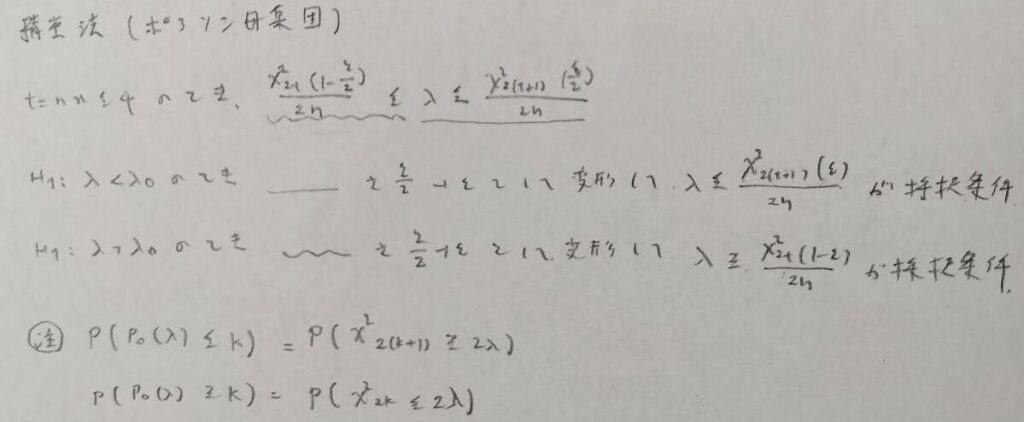
平成22年度問1(8)二項母集団における精密法(クロッパー・ピアソン法)

精密法から得られる信頼区間の左辺の分子はn2です。
精密法(母比率やポアソン分布のパラメータ)のときは、通常の感覚とは逆側の不等式を用いて片側検定を行います。ここの処理が検定では最難関です。

2023年度問5:二項母集団における精密法(クロッパー・ピアソン法)


本問もヘビーな難問です。数年前の難問より1つ問題が追加されているという本当にヘビーな量です。1つ言えることはF分布の確率密度関数を覚えていないと絶対に時間切れになることです。これはt分布にも言えます。一般には覚えなくても良い確率密度関数ですが、アクチュアリー数学を受験する際は暗記が必須になります。下記の本でしっかりと覚えるところは記憶して試験に臨みましょう!
平成29年度問3:ウェルチの検定


最難関の問題です。ウェルチの検定はやり方だけ覚えていれば良いと思われます。
2022年度問2(1)ウェルチの検定

アクチュアリー数学で最難関の年である2022年の問題です。第1問からウェルチの検定とは恐ろしいです。
この問題の恐ろしいところは、いつも素通りできるはずの前半の問題も難問であることです。
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。