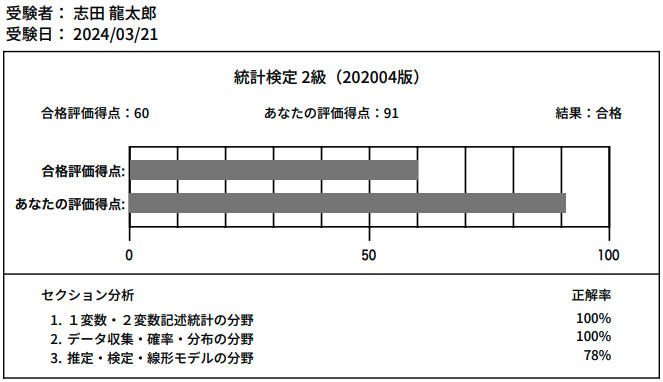
アクチュアリー数学で点推定と並んで頻出の区間推定を学びます。区間推定の方が公式をきちんと暗記できているか?が問われるので、アクチュアリー数学の花形の分野と言っても過言ではありません。
アクチュアリー数学の区間推定の問題はほとんど『確率統計演習 2 統計』から出題されています。そのためまずは『確率統計演習 2 統計』を解き切ることが大切です。
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
定義に従う新傾向問題
2022年問1(6)一様分布

アクチュアリー数学最難関のセットの問題です。最近でこのような問題が出ているので油断はできません。まずは信頼区間の定義をしっかりと理解して、次の節へと進んでいきましょう!
正規分布の期待値の区間推定
昭和63年度問4:一様分布

ワルドの方法の問題のため、広い意味で正規分布に関する問題としました。
平成元年度問1(5)誤差

アクチュアリー数学特有の頻出問題です。
平成元年度問1(6)母分散未知

t分布を使わせる問題で頻出問題です。
平成2年度問1(2)母比率の差の区間推定

こちらは正規母集団ではないので、母分散が未知というわけではありませんのでご注意ください。
平成2年度問1(3)誤差

問題文から母比率の問題だと気づく必要があります。
平成7年度問1(1)視聴率
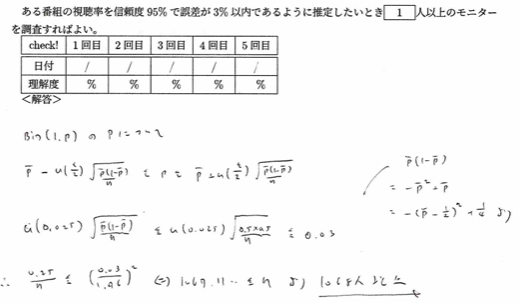
視聴率は母比率の問題としてとらえます。
平成7年度問4:信頼区間の幅

良問です。繰り返し学習しておきたい問題です。
良問だとは思いますが、難問でもあります。
平成8年度問1(3)対応のない場合

対応のある場合と比べてt分布の自由度が増えます。またプールした分散を用いることにも注意しましょう。この問題は実は統計検定2級レベルです。
平成9年度問1(2)母比率

少なくとも0.99の確率で〜は0.99の確率の時を考えれば十分です。
今回は定義域があるので、平方完成した後に注意します。
平成11年度問1(1)ロット
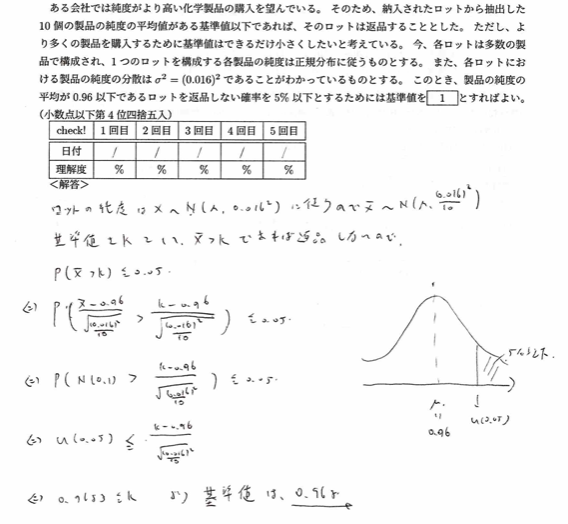
よく問題を読んで各種文字の設定を行いましょう。また、解答最初に求める確率の関係式を書いた方が標準化しやすいです。
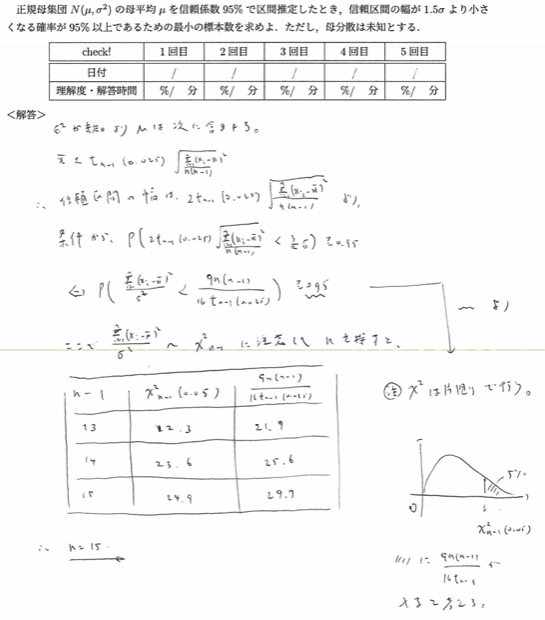
平成11年度問1(5)最小の標本数

本問は良問です。なぜならカイ2乗分布の考えを用いるためです。しっかりと確信を持って式変形できるように訓練しておきたい問題です。
平成12年度問2(2)標本数

平成15年度問2(2)信頼区間の幅の最小値

平成15年度問2(5)変化球

二項母集団は二項試行が無数に繰り返されることで形成される母集団全体を指し、二項分布はその母集団から一定回数の試行を行ったときの成功回数の分布を示すものです。用語の使い分けにも気をつけたいところですね。
難問です。無理やり標準正規分布を作り出すところや、厳しめに評価するために平方完成を用いるなど要点がたくさんあります。
平成15年度問4:大標本の判定

色々な知識を用いる総合的な問題です。
平成18年度問1(8)変化球

あまりないタイプの問題ですが、単なる計算問題になります。ここら辺の年は単純な計算をさせる問題が目立ちます。
平成20年度問1(6)支持率

色々と文字で置いていかないと解けません。近年頻出になってきているパターンです。
平成21年度問1(9)相関係数(z変換)

z変換を用いるタイプの相関係数の信頼区間の出し方は必ず記憶しておきましょう。
平成24年度問3:証明問題


平成27年度問1(7)対応のない分布

問題文から検定統計量をしっかりと見据えないと解けません。良問だと思います。
平成28年度問1(6)ポイント問題

見慣れない用語はよく問題文の定義を確認しましょう。今回はポイントの定義の確認が大切です。
2019年問1(7)ウェルチの近似法

本来は検定の章で扱うべきですが、区間推定の問題の流れに近いのでこちらで解説します。
ウェルチの近似法の式は頻度が少ないため、今後の出題が予想されます。公式はしっかり覚えておきましょう。
2019年度問3:証明問題


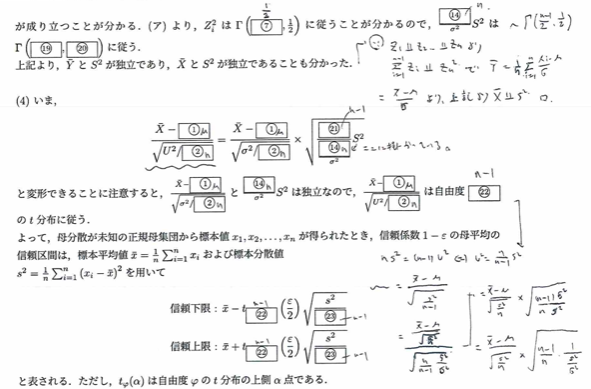
2020年度問1(6)典型問題
典型問題ですが混乱注意です。
2021年度問1(7)金額分散

正規分布の分散に関する区間推定(正規分布における母分散比など)
平成元年度問1(3)母分散比の区間推定

F分布の知識が要求されます。F分布については下記にまとめましたのでご覧ください。
平成14年度問4:検定との融合

平成21年度問1(7)測定された分散

求める内容が、どの分散か?に注意して考えましょう。要するに誤差を含んだものを求めるのか、誤差なしを求めるのか?の判定が大切です。
指数分布のパラメータの区間推定
平成7年度問3:典型問題

平成10年度問2(2)指数分布

平成12年度問2(4)典型問題

平成17年度問1(2)信頼区間の幅

平成26年度問3:指数分布


公式の確認問題です。
平成27年度問1(6)打ち切り

平成28年度問1(7)誤差問題

精密法(二項分布の母比率の区間推定)
平成9年度問1(4)発芽問題

精密法は公式を覚えるのはもちろんですが、理屈的にも導けることが重要になります。
左辺の分子がn2であることに注意しましょう!
平成14年度問2(5)変化球

平成19年度問3:証明問題


ここら辺の年度では最難関です。近年もこのレベルは典型問題として出題されています。
途中のk+1をkと直すところは、変数を置き換えているのではなく、単純に文字を置き換えているに過ぎません。また精密法の公式通り、nの添字がインデックスありとなしで入れ替わっていることにもご注意ください。それを見落とすと誘導に乗れません。
とにかく精密法(特に本問のような二項分布とF分布の関係を用いるパターン)は複雑ですので、『アクチュアリー試験 合格へのストラテジー 数学 第2版』で内容を整理しておくことをお勧めします。
平成27年度問3:F分布


精密法(ポアソン分布のパラメータの区間推定)
平成8年度問4:典型問題

初見では確実に解くのが不可能な問題です。予想だと2024年のアクチュアリー数学で類題が出る気がします。(2023年度が二項分布系だったため)
平成14年度問2(3)基本問題

平成29年度問1(5)近似法と精密法

近似法の場合はワルドの方法に沿って標準正規分布に従う統計量を考えます。そしてλの推定値(最尤法で求める)を代入すればOKです。精密法の方は分子の自由度が異なることに注意しましょう。
これで終わりですね。とても長かったです。
正規母集団の母平均の信頼区間などに関連する近似法が最もよく出題されていましたね。また区間推定は色々なバリエーションがあり、油断はできませんが、ここで得点できないと合格は苦しいです。しっかりと頑張りましょう!
アクチュアリー数学の区間推定の問題はほとんど『確率統計演習 2 統計』から出題されています。そのためまずは『確率統計演習 2 統計』を解き切ることが大切です。
全体的なおすすめの公式集は『アクチュアリー試験 合格へのストラテジー 数学 第2版』です。お手元に置いて本記事をご覧くだされば学習効率が上がります。