アクチュアリー数学は統計検定１級と比較可能な位の難易度の資格試験です。広範囲にわたるため中程度〜の過去問を分野ごとに解説します。
『アクチュアリー試験 合格へのストラテジー 数学 第2版』は合格に必須の公式が掲載されている唯一の参考書です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
ポアソン分布が合否を分ける問題として君臨しています。よくチェックしておきたいところですね。
ベルヌーイ分布
昭和63年度数学Ⅰ問５：分布関数
最初から難問です。アクチュアリー数学の分布関数関連の問題で最も場合分けが煩雑なタイプの問題です。
二項分布
平成15年度問１（２）複雑な式の分散
Yの取りうる範囲を求めるのが先決です。その後に確率分布を考えて分散を出していくことになります。パッと見すぐに終わりそうな問題ですが、時間がかかる良問です。
幾何分布
平成6年度数学Ⅰ問１（５）級数との融合
本問はとにかく期待値の中身を崩してから期待値計算を行う問題です。
平成10年度数学Ⅰ問１（８）追加費用の問題
ファーストサクセス分布
2019年度問１（１）表の多い方が勝ち
級数解法も理解しておきたい頻出問題です。
ポアソン分布
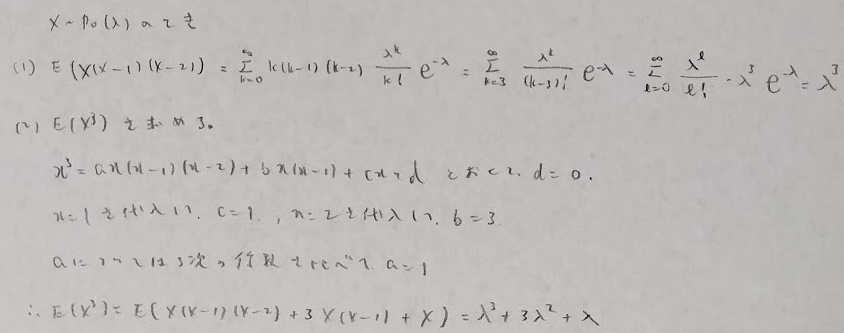
平成8年度数学Ⅰ問１（３）ポアソン分布の式に帰着
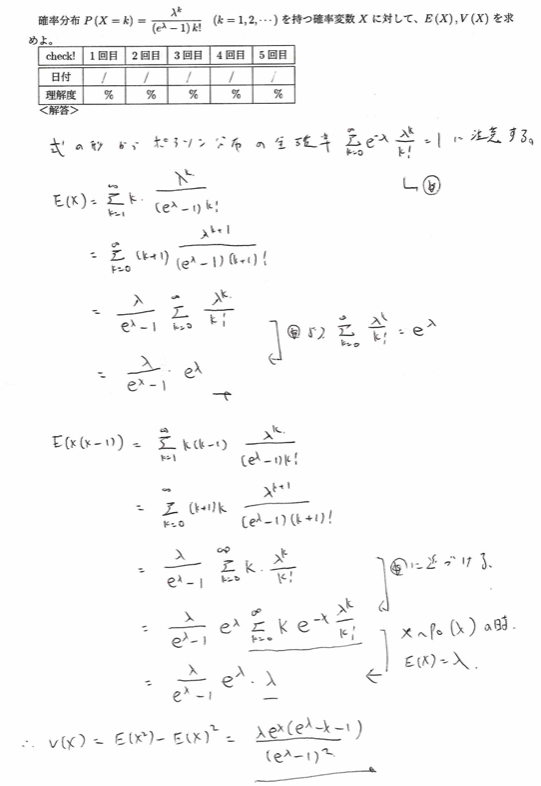
離散型確率分布は階乗モーメントを持ち出して分散を求めることが基本です。
平成9年度数学Ⅰ問４：指数分布との関連
本問は今後も出題が予想されます。Σと積分記号を用いた立式をスムーズにできるようにしたいですね。
平成10年度数学Ⅰ問４：バクテリア問題
ポアソン分布のパラメータを追っていくことがポイントです。また現時点のバクテリアの総数は、一体どこからやってきたのか？の着眼点を持つことが大切です。
平成16年度問３：歪度など
ガンマ分布のキュムラントを知っていると歪度は割と即答できます。指数分布の積率母関数なども瞬時に出しておきたいですね。公式暗記は必須です。
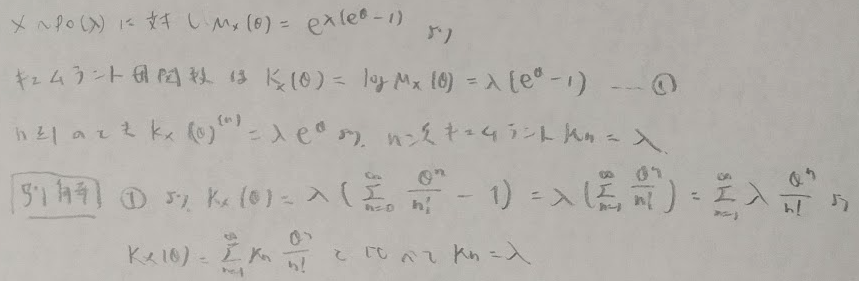
平成28年度問１（３）誠実さ問題
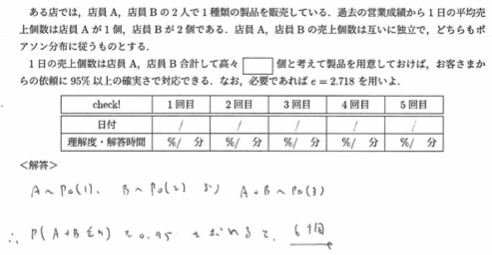
AとB合わせてn個以下の売り上げを出す確率が95%以上となるnは？という問題です。
言い換えがとてもややこしいですね。
2022年度問１（３）ポアソン少数の法則の見抜き方
npが一定でnを無限大にすると二項分布はパラメータnpのポアソン分布に従います。これをポアソンの少数法則と言います。本問ではnp＝３で一定であることに気づけるかの勝負です。
一様分布
平成8年度数学Ⅰ問２：ファーストサクセス分布との関連
離散一様分布の一般的なバージョンの期待値と分散の公式を覚えておきましょう。
平成11年度数学Ⅰ問４：特性関数
以後何回か出題されている有名問題です。マクローリン展開を積極的に使えるようにしましょう。
多項分布
平成11年度数学Ⅰ問２：ポアソン少数の法則の一般化
二項分布からポアソン分布を導く内容を一般化させた問題です。今後小問集合の中で後半の問題が問われることは十分あり得ます。
平成20年度問２：条件付分布
メインは（２）です。感覚的に答えが出せるようにしておきましょう。（３）は過去問と同問です。
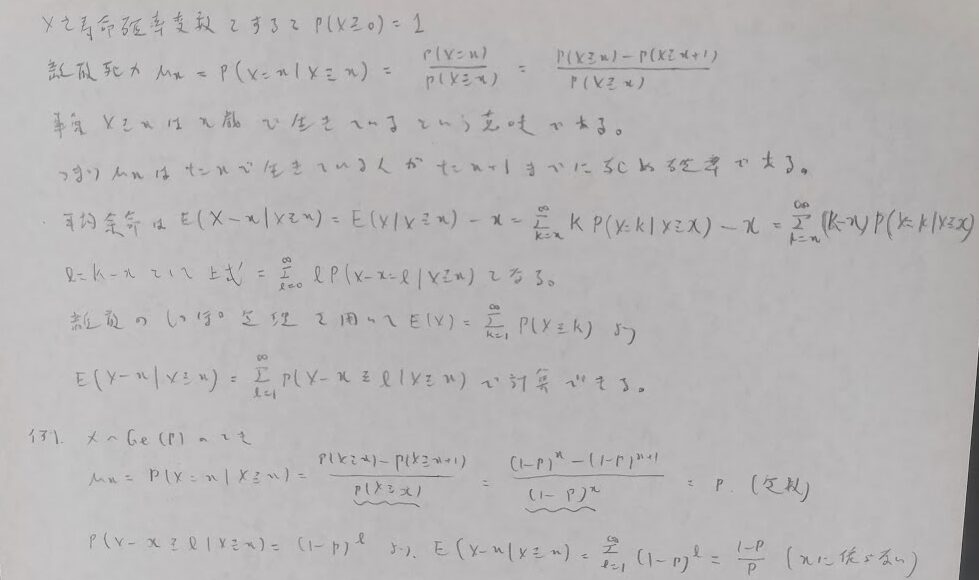
『アクチュアリー試験 合格へのストラテジー 数学 第2版』は合格に必須の公式が掲載されている唯一の参考書です。お手元に置いて本記事をご覧くだされば学習効率が上がります。
